题目一:判断一棵二叉树是否是完全二叉树
题目分析
层序遍历
将所有的结点加入队列(包括空结点)。当遇到空结点时,查看其后面是否有空结点。若有,则二叉树不是完全二叉树。如果是满二叉树或者完全二叉树,这些空结点应该是在广度优先遍历的末尾,所以,当我们遍历到空洞的时候,整个二叉树就遍历完了。但如果是非完全二叉树,当遍历到空结点时,空结点后面还有非空结点。
C++代码
1 | bool IsComplete(TreeNode* root){ |
题目二:计算二叉树双分支结点个数
题目分析
计算一棵二叉树中的所有双分支结点个数的递归模型$f(b)$如下:
$f(b)=0$ 若b=NULL
$f(b)=f(b->left)+f(b->right)+1$ 若*b为双分支结点
$f(b)=f(b->left)+f(b->right$) 其他情况(*b为单分支结点或者为叶子结点)
C++代码
1 | int double(TreeNode* root){ |
题目三:访问先序遍历第k个节点
题目分析
递归
C++代码
1 | TreeNode* dfs(TreeNode* root,int &k){ |
题目四:打印某个结点的所有祖先
题目分析
递归
C++代码
1 | bool printAncestor(TreeNode* root,int target){ |
题目五:求二叉树的宽度
题目分析
层序遍历
C++代码
1 | int TreeWidth(TreeNode* root){ |
题目六:KMP算法
求next数组
next[j]表示当模式串匹配到T[j]遇到失败时,在模式串中需要重新和主串匹配的位置。换言之,next数组的求解实际是对每个位置找到最长的公共前缀下面按照递推的思想总结一下求解next[]数组:
- 根据定义next[1]=0,假设next[j]=k, 即P[1…k-1]==P[j-k,j-1]
- 若P[j]==P[k],则有P[1..k]==P[j-k,j],很显然,如果next[j]=k; 则next[j+1]=next[j]+1=k+1;否则next[j+1]=k+1!=next[j]+1;
- 若P[j]!=P[k],则可以把其看做模式匹配的问题,即匹配失败的时候,k值如何移动,显然k=next[k]。
1 | void get_next(char T[],int next[]){ |
KMP算法
时间复杂度O(m+n)
1 | public static int KMP(String ts, String ps) { |
题目七:排序算法
插入排序
基本思想:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子序列中,直到全部记录插入完成
直接插入排序
1 | void InsertSort(int A[],int n){ |
设置哨兵的作用:避免数组下标出界
直接插入排序是边查找边移动
折半插入排序
1 | void InsertSort(int A[],int n){ |
折半插入排序是先查找再移动
希尔排序
1 | void shellsort1(int a[], int n) |
交换排序
冒泡排序
1 | void BubbleSort(int A[],int n){ |
快速排序
1 | int Partition(int A[],int low,int high){ |
空间效率:由于快速排序是递归的,需要借助一个递归栈来保存每一层递归调用的必要信息,其容量与递归调用的最大深度一致。最好的情况下为$log_2(n+1)$;最坏情况下,因为要进行n-1次递归调用,所以栈的深度为$O(n)$;平均情况下,栈的深度为$O(log_2n)$
应用
双向冒泡排序
奇数趟的时候,从前往后比较相邻元素的关键字,遇到逆序即交换,直到把序列中关键字最大的元素移动到序列尾部。偶数趟时,从后往前比较相邻元素的关键字,遇到逆序即交换,直到把序列中关键字最小的元素移动到序列前端。
1 | void BubbleSort(int A[],int n){ |
寻找数组中第k小的元素
从数组L[1…n]中选择枢纽pivot(随机地或者直接取第一个)进行和快速排序一样的划分操作后,表L[1…n]被划分为L[1…m-1]和L[m+1…n],其中L[m]=pivot
讨论m与k的大小关系:
- 当m=k时,显然pivot就是要寻找到的元素,直接返回pivot就可以
- 当m<k时,则要寻找的元素一定是在L[m+1…n]中,从而可以对L[m+1…n]递归地查找第k-m小的元素
- 当m>k时,则要寻找的元素一定是在L[1…m-1]中,从而可以对L[1…m-1]递归地找第k小的元素
该算法的时间复杂度在平均的情况下可以达到O(n)
1 | int kth_elem(int A[],int low,int high){ |
选择排序
每一趟(例如第i趟)在后面n-i+1(i=1,2,..,n-1)个待排序元素中选取关键字最小的元素,作为有序子序列的第i个元素
简单选择排序
基本思想:假设排序表为L[1...n],第i趟排序即从L[i...n]中选择关键字最小的元素与L[i]交换,每一趟排序可以确定一个元素的最终位置,这样经过n-1趟就可以使得整个排序表有序
1 | void Selectsort(int A[],int n){ |
堆排序
1 | priority_queue<int> heap_max; //定义大根堆 |
归并排序
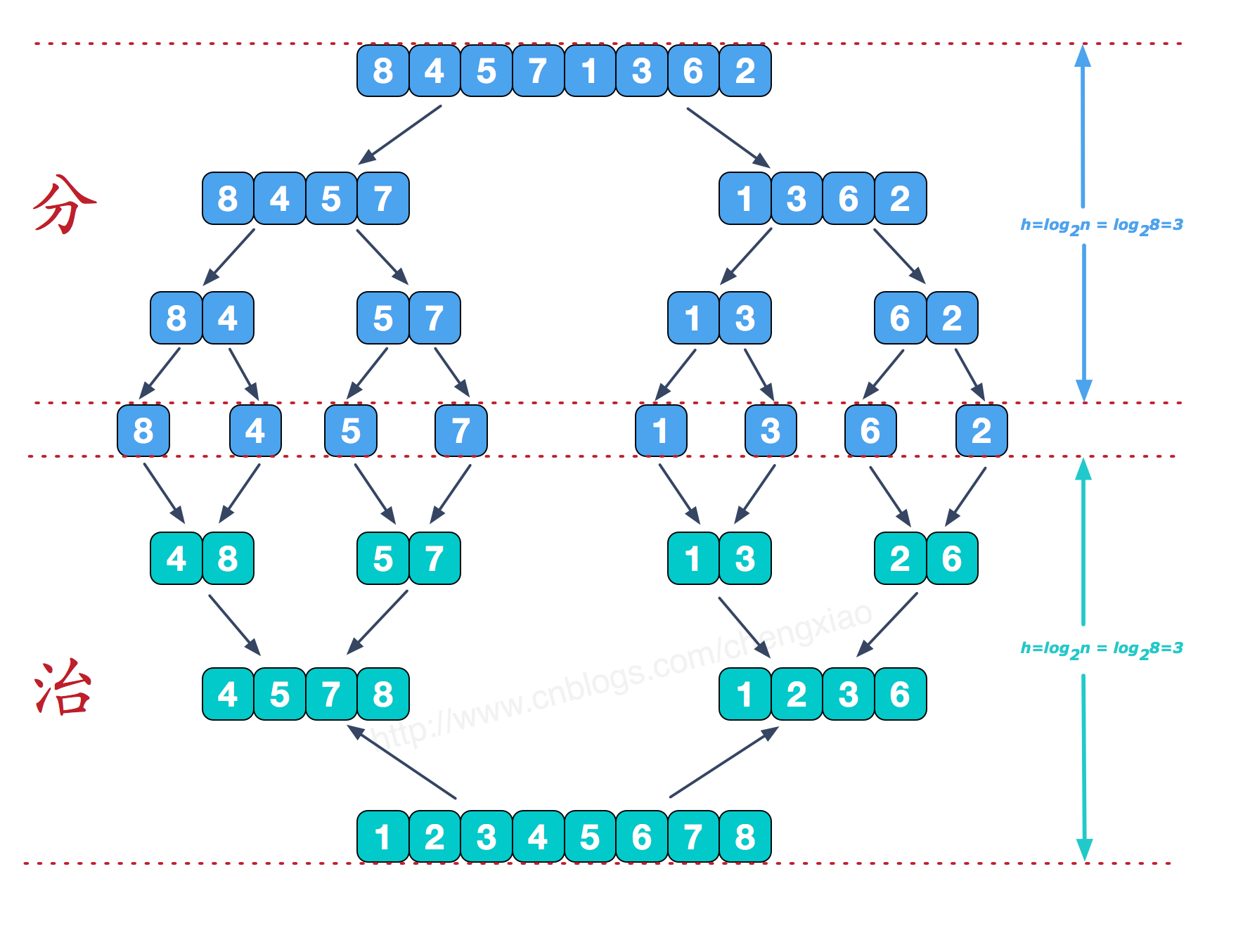
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起,即分而治之)。
1 | vector<int> B; |
各种排序算法的性质

非递归访问数
首先要想到用到栈这个数据结构,其次要搞清楚递归的顺序
前序非递归遍历
1 | void preOrder2(BinTree *root) //非递归前序遍历 |
中序非递归遍历
1 | void InOrder(BiTree *T){ |
后续非递归遍历
1 | //strcut TreeNode { |
