MuMaXu's Blog

摘要

这份报告总结了作为INRIA实习的一部分所完成的工作，作为完成数学和信息学硕士学位的部分要求。这次实习的目的是开发一个软件环境来模拟电网中的电力传输和操作人员维护电网安全的行动。我们的环境通过增强学习(RL[1])代理自动控制电网，帮助人类操作员。它能够组织基准测试，包括INRIA和RTE计划于2019年在机器学习方面发起的一项挑战。我们的框架，基于开源库(Matpower[2])不久将在Github上公开。在这份报告中，我们介绍了中介结果及其在强化学习(RL)游戏中的应用。

介绍

本项目涉及与特高压和高压电网(63kV及以上)输电有关的技术问题，例如由法国TSO(输电系统运营商)RTE (R’eseau de Transport d’electricit’e)公司管理的电网。从智能电网技术在配电网络中的应用到更精确的消费预测工具，能源基础设施的效率将在未来十年得到大量的提高。随着我们在利用风能和太阳能将可再生能源转化为电能方面取得的进展，我们还将看到电力需求的增长，如电动汽车。众所周知，电力很难储存在工业水平上。因此，电网的供需必须在任何时候都尽可能地保持平衡。如果不能达到这一平衡，可能会导致网络故障和随后不同程度的停电。基本上，关闭和重新启动发电厂(特别是核电厂)是非常困难和昂贵的，因为没有简单的方法来开关发电机。许多消费者，包括医院和在家中住院的人，以及工厂，都面临着严重的断电问题。使用机器学习(特别是强化学习)可以让我们更好地优化电网的运行，最终减少输电线路的冗余，更好地利用发电机，降低电价。这个项目的目标是准备一个数据科学挑战，让科学界参与进来，帮助解决这个难题

RTE是一个传输系统运营商(TSO)。TSOs的目标之一是在避免设备故障的约束下，利用电网将电力从生产转到消费。我们感兴趣的一个典型故障是由过热引起的线路意外停机。当线路受到大于名义阈值的功率流影响时，就会发生这种事故。为了避免线路故障(以及可能的后续级联故障)，操作员(调度程序)有一组可供处理的操作:他们可以在本地修改线路互连、接通或关闭电力线，或更改电力生产。

这项任务的困难在于网络架构(也称为网格拓扑)的复杂性，它经常由于硬件故障(例如雷暴等天气条件)、计划的维护或预防措施等事件而发生变化。最重要的是，可再生能源的发展比传统的生产系统(如核电站)更难预测，给生产计划带来了更多的不确定性。在这种情况下，我们有兴趣开发工具，以帮助调度人员维护电网的安全，并面对日益复杂的任务。这项工作是在Benjamin Donnot[3][4][5]博士论文和Joao Araujo(去年夏天对该课题进行了初步研究的实习生)工作的基础上进行的。

最近在深度学习[6]方面的工作已经强调了深度神经网络在解决复杂任务方面的潜力([7]，[8])。对于分类和回归任务，它们通常使用监督学习进行训练，这需要一个标记的数据集。在我们的例子中，一个合适的数据集可以由网格情况和调度程序的处理动作组成，这样模型就可以通过复制(希望是一般化的)给定网格状态的调度程序动作来训练。不幸的是，我们无法访问这些标记的数据，这些数据为特定的危机情况提供调度程序的预防或补救措施，用于非常高电压的电网1。

这促使我们研究强化学习的方法。最近的论文([9]，[10]，[11])成功地将强化学习应用于高维时间任务。我们的问题的一个具体方面是，在一些非常严格的假设下(例如我们处于准静态状态)，可以使用实现物理定律(常微分方程)的物理模拟器精确地模拟电网。这些假设在电力系统中很常见。因此，我们的问题很适合于强化学习，因为数据可以使用环境模拟器(电网物理模拟器)生成。人们希望一个经过训练的模型能够实现一个策略(将网络状态映射到在一段时间内保持网络安全的预防或治疗操作)，这个策略可以用来帮助人类调度程序做出正确的决策。在我们的项目中，我们通过将自己限制在网格和动作子集的玩具示例中来简化整个问题，从而创建一个模拟电网控制的半现实条件的“严肃游戏”。这个游戏有助于强化学习解决方案。拟议的框架将用于在Codalab平台上实现的挑战(http://competitions.codalab.org)。

本文件组织如下。首先，我们给出了一些关于电网和大规模电网运行的背景。其次，我们回顾了近年来机器学习在电力系统和强化学习中的应用。然后介绍我们对框架的设计和实现的贡献。接下来的部分讨论了使用所提出的对策所获得的一些早期结果。最后，最后一部分列出了未来工作的关键要素。

背景

Power grids

电网是由电力硬件构成的网络，其目的是将电力从生产设备传输到消费设备。电网的表示如图1所示。形式上，一个电网的结构是一个图$G={V,E}$;例如，用V表示节点集，用E表示边集。边表示电力线，也称为支路或传输线。在实践中，V是变电站的集合，变电站是其他元素可以相互连接的物理实体，如生产(如太阳能发电厂)或消耗(如城市)。总线是一个数学概念，指的是变电站内直接连接的元素的交集。变电站可以有多个总线，即元素可以直接连接到其他元素的任何子集。图2显示了由4个元素组成的变电站的两种表示:一个发电机$G$，一个消耗$C$，两条电力线$L1$和$L2$。在这个特殊的拓扑结构中，有2个总线:由$G$和$L1$组成的总线和由$C$和$L2$组成的总线。注意，总线没有适当的物理表示:因此，2中的两个表示是严格等价的(总线排列的不变性)。

具体地说，变电站是由电线杆构成的，在电线杆上可连接的元件可以接通。TSOs的技术人员可以通过操作开关改变连接元件的电杆。它们还可以关闭诸如分支之类的元素，以便将它们暂时从网格中移除(例如，重新绘制电力线)。此外，不可能只有一个元件连接到一个极点，因为电力将没有出口点。在这项工作中，我们将限制变电站最多有两个总线，即变电站的元素可以分为最多两个组，其中对象是直接连接的。换句话说，每个变电站的元件可以连接成一组或两组。

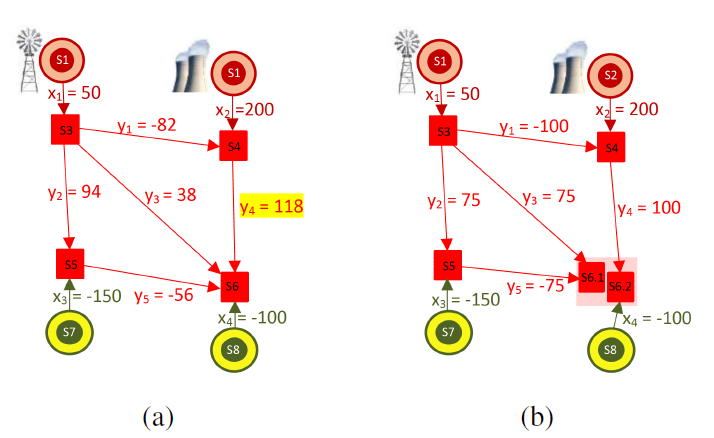
图1:输电网小实例

电力必须从生产节点(棕色圆圈)传输到消耗节点(绿色圆圈)。它们通过传输线(红线)组成的网络(网格)相互连接，在变电站(红方)进行连接。$X=\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$包括生产和消费的x4)加起来等于零。线相互连接的方式称为网格拓扑 $\tau$ 。红线Y中的流动是由注入和拓扑结构产生的:$Y=S(X, \tau)$.在任何时候，电网运营商(或调度员)必须确保网络安全运行，不允许任何线路超过其热极限(超过热极限的电流可能导致线路熔化)。(a)直线$y_4$超过了它的热极限100。(b)拓扑结构的变化(节点6的分裂)使$y_4$回到其热极限。

在图结构的顶部，一个电网被提交给基尔霍夫定律。例如，在任何节点上，输入功率之和等于输出功率之和。给定一组注入(产量和消耗值)、网络结构和物理定律，网格将自然收敛到平衡状态，也称为稳态。我们特别感兴趣的是稳定状态下网格分支中循环的流动。

电流的值是由支路的实功率和无功功率与支路所在变电站的电压值组合而成。支路实功率的集合通常记为P，无功功率为Q, V为对应的电压幅值。

Safety criteria and grid conduct

TSO的调度程序需要确保电网始终在安全的条件下运行。出于这项工作的目的，当没有分支处于溢出状态时，网格将被认为是安全的。实际上，采取了一种更严格的方法。TSOs经常确保，如果电网的一个组件发生故障(例如一个分支、一个工厂或一个开关)，那么整个电网将保持安全，即没有分支溢出。对这一现实标准的验证将需要大量额外的计算资源，这就是我们在研究中没有考虑到这一点的原因。当支路的流动电流超过其热阈值时，支路就会溢出。电力线中的电流越大，其受热程度越高，从而引起电力线的膨胀现象。线路与地面之间的空气起到绝缘作用，可能不足以保护附近的乘客免受电弧的伤害。除了乘客的安全外，融化的电源线也需要更换。在高电压电网中，更换线路需要几周时间，而这样的更换可能要花费数百万欧元。系统的每条线都有一个名义的热极限，在这个极限下，系统就不会熔化。通过表示b支路电流$f_b$值和$th_b$热限$th_b$，溢流对应于:

$$b \text { overflowed } \Longleftrightarrow f_{b} \geq \mathrm{th}_{b} \Longleftrightarrow \frac{f_{b}}{\mathrm{th}_{b}} \geq 1$$

调度程序有一组操作供其使用，以避免在电网出现故障时进行操作。基本上有三种类型的行动:

• 打开/关闭分支。

• 改进发电机的电力生产。

• 节点分裂。

在全国范围内的电网中，经常使用分支断开或重新连接的方法，但调度员很少使用这种方法。当一个支路溢出时，系统会自动断开后一个支路，这样它就不会熔化。从理论上讲，调度程序可以在预测的故障发生溢出之前断开一个分支。开关一个分支操作是便宜的，因为TSOs操作在他们的范围内的元素(例如激活开关修改分支互连)。在实际操作中，调度员不会为了维修或喷漆等维护操作而断开电源线。实际上，电网的电力容量只有在某些支路被切断时才会降低(与完全运行的电网相比)，这意味着电网更容易发生溢流。

修改产品输出，通常称为重新调度，是改变某些产品所产生的能量量的操作。这些操作称为“重新调度”，因为一个产品降低了给定的数量，然后在其他产品之间重新分配。如果数量不平衡，可能就没有足够的产品来满足需求。重新调度是昂贵的，因为这种操作需要修改多个发电机，这不是TSOs的属性。

因此，我们在这项工作中不考虑重新调度。节点分割表示由RTE上的调度程序执行的大多数人工干预。它是改变变电站内部元件的互连配置的操作。根据定义，变电站是至少两个分支的交汇处。事实上，分支只能连接到变电站分支的一个子组。节点分裂的操作包括修改分支互连的模式。该名称指的是将操作视为对变电站的子节点(或总线)的定义，每个分支都不连接一个子节点或一个子节点。在下面的代码中，我们将子节点的数量限制为2。

大规模电网的运行方式主要有两种:

• 一种预防模式:在对生产和消费方案进行估计的情况下避免未来的失败

• 治疗模式:根据当前的网格负载流解决故障

RTE的调度程序经常确保电网当前处于安全状态，即没有故障。如果发生故障，调度程序将执行补救措施。在常规模式下，没有事故，他们有一个预期的工作模式。事实上，调度员经常确保“n-1”标准得到遵守。这个标准意味着如果网格中的任何元素失败，那么网格仍然是安全的。通常，他们会对当前的网格进行多次模拟，但其中一个元素已经停止工作，观察潜在网格的稳定状态。实施这个标准是因为意外的危险可能发生并破坏电网的某些部分，如电力线。参见Donnot关于使用深度学习来预测“n-1”情况下网格的流以加速这些模拟的工作[12]。

TSOs通常在国家范围内运作。例如，RTE操作由6500个节点、3000个产品和10000个分支组成的法国网格。考虑到危险、维护和注入分布，在安全模式下运行电网的任务相当复杂。此外，人为因素限制了用于预测网格后续状态的工具。例如，在管理网格时可以集成温度估计和天气预报，但这只会使调度程序的任务变得复杂。In context, 我们感兴趣的是建立一个政策 $\Pi$ : $$
S \rightarrow A

$$(S是状态集，A是动作集)，它会给出给定网格状态的多个解决方案，这样操作人员可以通过在候选操作中选择一个操作来快速做出决策。 ## Load-flow computations 负载流计算是在给定网格结构、一组注入和一组描述产生、负载、分支和其他元素的参数的情况下，计算电网内流值的操作。我们假设一个受注入作用的网格会瞬间收敛到它的稳态。 因此，潮流计算是一个受等式和约束的优化问题，需要几十个变量来描述电网的元素，如电力线的电阻、电抗。大多数高压电网是在交流模式(交流电流)下运行，而不是在直流模式(直流电流)下运行。然而，交流负载流是复杂和缓慢的计算，他们有时用直流近似。 The DC 建模 使 以下 简化 assumptions: - 分支是无损的:分支的输入和输出功率是相同的。 - 所有的总线电压都接近1个单位。 - 支路电压角几乎相同。 所有这3个假设使得初始问题线性化，如附录二所示。使这个问题线性化有一些优点，包括计算时间短。 另一方面，AC模型并没有对系统进行先前的简化假设。因此，交流模拟比直流模拟更接近实际情况。However, AC负载流量计算比DC, 更难 , 因为 整个方程非线性 (举例来说, 如果角度x的区别不是接近 0 , 然后$\sin (x) \approx x$, sin是非线性的). 多种优化算法可用于交流潮流计算，包括牛顿法、快速解耦法或高斯塞德尔法。 我们的框架依赖于Matpower[2]，这是一个用Matlab编写的开源电力系统框架。Matpower与IEEE电网格式兼容。有关此格式的详细信息，请参阅附录I。 ## Examples of power grids 对于电网控制的第一次强化学习挑战，整个法国电网可能过于雄心勃勃，因为我们认为元素的数量(即负荷流的维数)对于当前的强化学习方法(大约6500个节点和近10000行)来说过于庞大。 加州输电网是一个相对简单的系统，已经被广泛研究，如[13]，[14]或[15]。此网格的一些简化实现以开放源代码(和IEEE格式)提供。这些实现定义了关于网格元素的各种参数，包括网格结构。各种版本存在。我们对iee -118案例特别感兴趣，它是对加利福尼亚网格的简化。在意大利，它有118个变电站，56个产品和186个分支机构(不包括产品和变电站之间的线路)。 ## Reinforcement learning 强化学习(RL，[1]，[16])是一个不同于监督学习和非监督学习的机器学习领域。确实，在强化学习中没有监督者，而是一个奖励信号，在我们的例子中表示网格安全约束的满足程度。一个代理(在我们的例子中是模拟调度程序)与环境(在我们的例子中是游戏)进行交互，实现一个策略来决定在给定的状态下执行哪些操作，从而实现回报最大化。RL算法训练一个策略，该策略通常是系统状态和奖励的一个参数函数。本例中的操作集取自网格拓扑中允许的更改。RL系统通常用马尔可夫决策过程(MDP)来描述。马尔可夫决策过程是一个元组$\langle S, A, P, R, \gamma\rangle$;我这样: - S是状态的有限集 - A是一个有限的动作集合 - P是状态转移概率矩阵，$P_{s s^{\prime}}^{a}=\mathbb{P}\left[s_{t+1}=s^{\prime} | s_{t}=s, a_{t}=a\right]$ - R是奖励函数，$R_{s}^{a}=\mathbb{E}\left[R_{t+1} | s_{t}=s, a_{t}=a\right]$ - $\gamma$是折扣因子$0 \leq \gamma \leq 1$ 在这里策略$\Pi$充分 描述了代理人 的行为作为一个分布的行动空间 states:$$

\Pi(a | s)=\mathbb{P}\left[a_{t}=a | s_{t}=s\right]

$$MDP的所有状态都是马尔科夫的，也就是说，在当前的情况下，未来是独立于过去的，其形式化形式为:$$

s_{t} \text { is Markov } \Longleftrightarrow \mathbb{P}\left[s_{t+1} | s_{t}\right]=\mathbb{P}\left[s_{t+1} | s_{1}, \ldots, s_{t}\right]

$$MDP的回报$G_t$为从时间步t开始的累计折扣奖励:$$

G_{t}=R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots=\sum_{k=0}^{\mathrm{inf}} \gamma^{k} R_{t+1+k}

$$从回报中我们定义两个值函数: - 在给定状态$S$下策略$\Pi$的状态价值函数为：$v_{\Pi}(s)=\mathbb{E}\left[G_{t} | s_{t}=s\right]$ - 在给定应用在状态$S$的动作$a$下策略$\Pi$的动作价值函数为： $q_{\Pi}(s, a)=\mathbb{E}\left[G_{t} | s_{t}=s, a_{t}=a\right]$ 进一步定义最优状态值函数$v *(s)$和最优行为价值函数$q *(s, a)$分别为状态价值函数和动作价值函数策略的最大值:$$

v (s)=\max _{\Pi} v_{\Pi}(s) q (s, a)=\max _{\Pi} q_{\Pi}(s, a)

$$MDPs存在多种变体。例如，无限的MDP可以包含连续的状态空间或动作空间。部分可观察的MDP涉及一个不直接观察状态的代理。 最优值函数描述了MDP中可实现的最佳性能，从而解决了这个问题。我们可以证明存在一个最优解:它的性能大于或等于任何其他模型。这种最优策略在状态值和动作值函数方面都具有本质上的最优性。 MDPs的优势在于其执行顺序决策的能力:时间数据在强化学习中很重要(因为延迟的奖励)，因此数据不需要是独立的和同分布的。 强化学习的整体机制在于通过与环境的交互来训练代理。在每个时间步t,代理需要一组动作集合$a_t$从一个动作空间中,基于$s_t$环境的当前状态和之前的奖励$R_t$。环境然后计算下一个状态$s_{t+1}$以及奖励$R_{t+1}$ 根据$s_t$和$a_t$。图3给出了这种普通机构的可视化表示。  # 技术发展最新水平 ## 机器学习应用于电力系统 强化学习绝不是将机器学习应用于电力系统的唯一方法。还有许多其他方法可以将机器学习应用到电力系统中，这些方法不一定是用来控制电力系统，而是用来预测电力流，而不是使用精确但速度缓慢的物理模拟器，如Matpower或不能正确使用gpu的更复杂的模拟器。机器学习的一个优点是，我们不需要像通常的负载流软件那样明确系统的规则。该模型可以在不需要任何领域知识的情况下学习物理概念的内部表示。 机器学习已被应用于电力系统问题。为了取代传统的基于微分方程求解器的仿真器，提出了一种新的深度学习算法来计算负载流。他们的方法在于训练前馈多层感知器在给定网格预测load-flows一行关闭。他们的泛化算法的计算loadflows两条线在哪里断开连接(培训歧管的网格与一个且只有一个关闭线)。 他们的方法依赖于一种新颖的架构调用引导退出。它受深度学习中常用的传统辍学[17]的影响。但是，它们采用了一种基于输入控制活动单元的方案，而不是随机地使一些隐藏单元无效。更准确地说，他们用一组结果、一组负载和线路服务状态(开关或关闭)的二进制向量作为输入，构建了一个前馈神经网络。该模型输出一组流，这些流应该接近基本事实流。该模型使用反向传播进行训练，并带有均方根误差等回归损失。在这种情况下，一些隐藏的单元只在相关的线路断开时才被激活，即相关的线路连接状态输入为0。他们的方法比基线方法有更好的训练和测试性能，基线方法包含在相同的网络中，没有引导退出，即所有有条件激活的单元都被激活(有更多的参数，所以更大的容量)。 神经网络也被用于短期负荷预测([18]，[19])。其上的思想是更好地预测消耗方案，这样由于更好的估计器，可以更好地预测电网未来状态。最近的挑战see4c (http://project.see4c.eu/)是机器学习与电力系统集成的另一项工作。挑战的目标是根据历史数据预测电力流量。 ## 强化学习近期工作 在这里，我们提出一些算法和概念用于强化学习处理复杂系统，在游戏的背景下。 1）深度Q-learning on Atari games:谷歌DeepMind已经成功地使用了深度Q-learning来处理Atari 2600游戏[20]的任务，这是一款街机游戏的集合。游戏通常是在街机,大致包括屏幕用来移动一个对象有一个操纵杆在四维空间(左/右/上/下),和一个按钮来执行一个特定的行动基于游戏的类型(例如在太空入侵者发射激光)。他们的模型在几个遗传算法上实现了超人的性能 深度Q-learning on Atari games:谷歌DeepMind已经成功地使用了深度Q-learning来处理Atari 2600游戏[20]的任务，这是一款街机游戏的集合。游戏通常是在街机,大致包括屏幕用来移动一个对象有一个操纵杆在四维空间(左/右/上/下),和一个按钮来执行一个特定的行动基于游戏的类型(例如在太空入侵者发射激光)。他们的模型在几款游戏中实现了超人的表现，可以玩上千种不同的游戏。 为此，他们首先对一个价值函数$Q(s;a)$使用深度神经网络，其中s为状态，a为动作。更准确地说，该网络是一个具有ReLU[22]激活的卷积神经网络[21]。网络输入由4个连续堆叠的帧组成(从游戏模拟器获得)，因此在输入中有一个运动的概念。网络输出由一个大小为5的向量组成，表示按下了哪些按钮。 在这种建模之下，在每一个时间步t的状态$s_t$下，动作$a_{t+1}$的发生是为了最大化期望的Q函数：$$

a *_{t+1}=\underbrace{\operatorname{argmax}_{a \in A}} Q\left(s_{t}, a\right)

$$
2）AlphaGo:过去十年，人工智能领域最重要的突破之一是人工智能战胜了围棋世界冠军。围棋是一种零和游戏，棋盘大小19乘19。在每个非使用的位置，玩家可以放置他们的棋子。游戏的目标是控制更大的棋盘区域。在过去，人们已经建立了几个次人类的性能模型，主要是基于树搜索算法，并通过交易近似与树深度探索来增强。围棋游戏非常难以详尽地模拟国际象棋，因为围棋棋盘更大。对于一个很小的n, 大约 有$(19 \times 19)^{n} 81^{n}$可配置从当前 网格 的 网格 n depth, 迅速超出当前计算机计算能力的范围。

游戏设计