Leetcode动态规划算法专题

发表于 | 分类于 ，

问题一：Triangle

问题描述

给定一个三角形，找到从上到下的最小路径和，在每一步可以移动到下一行的相邻数字。

Bonus: 只使用$O(n)$额外空间，其中n是三角形的总行数

样例
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
输出11 (2 + 3 + 5 + 1 = 11).

问题分析

动态规划 时间$O(n2)$空间$O(1)$

点$(i,j)$的下一行的相邻数字是$(i+1,j)$和$(i+1,j+1)$。

$f(i,j)$表示从下往上走到位置$(i,j)$时的最小路径和，计算方式/状态转移方程是

$f(i,j)=minf(i+1,j),f(i+1,j+1)+(i,j)$

之所以要从下往上走的原因是因为最上面只有一个元素，就可以直接表示为我们的最终组织，如果是取最底下一行的话，还要进行判断。

复杂度分析：

直接把$f(i,j)$存在位置$(i,j)$处，不使用额外空间，因此空间复杂度为$O(1)$。

两层for loop，第一次竖着遍历，第二次横着遍历，时间复杂度为$O(n^2)$。

样例：

输入
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
更新后

[
     [11],
    [9,10],
   [7,6,10],
  [4,1,8,3]
]

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
    	int m=triangle.size();
    	for(int i=m-2;i>=0;i--)
    		for(int j=0;j<triangle[i].size();j++)
    		{
  				triangle[i][j]=max(triangle[i+1][j],triangle[i+1][j+1])+triangle[i][j];
			}
		return triangle[0][0];
	}
};

问题二：Unique Paths II

问题描述

是62题Unique Paths的进阶版，考虑在网格中加入了障碍，在网格图中，0该网格是空的，1表示该网格有障碍，例如

1
2
3
4
5
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

这样一个网格，不能经过中间的格子，从左上角到右下角的路线数目为2.

样例

1
2
3
4
5
6
7
8
输入：网格的0 1矩阵
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
输出：2
解释：不能经过中间的格子，从左上角到右下角的路线数目为2

问题分析

(动态规划)$ O(mn)$

类似于62题Unique Paths，每一个网格都可以由该网格左边或上边的网格转移过来，因此到达某一点的路径数等于到达它上一点的路径数与它左边的路径数之和，不同的是，当某个网格有障碍时，到达该网格的路径数为0。这还是一个递推问题，考虑用动态规划。动态规划数组dp[i][j]= 起点到点(i, j)的路径总数。于是我们就得到递推关系式：当网格为0时，dp[i][j] = dp[i][j-1] + dp[i-1][j]；当网格为1（说明该网格是障碍物），dp[i][j]=0。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& nums) {
      	if(nums.empty()) return 0;
    	int m=nums.size();
    	int n=nums[0].size();
    	vector<vector<int>> f(m,vector<int>(n));
    	f[0][0]=1;
    	for(int i=0;i<m;i++)
    		for(int j=0;j<n;j++){
  				if(dp[i][j]==0){
  					if(i) f[i][j]+=f[i-1][j];
  					if(j) f[i][j]+=f[i][j-1];
				}
				else
					f[i][j]=0
			}
		return f[m-1][n-1];
	}
};

问题三：Russian Doll Envelopes

问题描述

你有一堆信封，并且已知它们的宽和长(w, h)。如果一个信封的长和宽都小于另一个信封，那就可以将这个信封放到那个信封中。

现在以俄罗斯套娃的方式将这些信封装起来，问最多可以装几层？

样例

给定信封：[[5,4],[6,4],[6,7],[2,3]]，
则最多可以套3层。
解释：[2,3] => [5,4] => [6,7]

问题分析

(动态规划) $O(n^2)$

先将所有信封按宽的长度从小到大排序，然后问题变成从左到右找一条最长的h严格单调递增的子序列，同时满足w也是严格单调递增的。

类似于最长上升序列问题，可以用动态规划解决。

状态表示：f[i] 表示以第i个信封为结尾的单调序列的最大长度。
状态转移：对于f[i]，枚举j=0∼i−1，如果第 j个信封的长和宽都小于第i个信封，则用 f[j]+1更新f[i]。

时间复杂度分析：排序部分的时间复杂度是O(nlogn)。动态规划部分一共有n个状态，每个状态进行转移的计算量是O(n)，所以动态规划的时间复杂度是$O(n^2)$。总时间复杂度是$O(n^2+nlogn)=O(n^2)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool 
class Solution {
public:
    int maxEnvelopes(vector<pair<int, int>>& envelopes) {
    	sort(envelopes.begin(),envelopes.end());
    	int m=envelopes.size();
    	vector<int> f(m);
    	int res=0;
    	for(int i=0;i<m;i++)
    		f[i]=1;
    		for(int j=0;j<i;j++){
    			if(envelopes[i].first>envelopes[j].first&&
    			envelopes[i].second>envelopes[i].second){
  					f[i]=max(f[i],f[j]+1);
				}
			}
			res=max(res,f[i]);
		return res;
	}
};

总结

在动态规划中一定要满足后面的状态可以从前面的状态中推得出来，这里也就是说状态的转移要具有顺序性

在这个题目中有条件j<i就可以满足顺序性，是由前面所有的状态递推此刻的状态，然后取极值。

问题四：Counting Bits

问题描述

给定一个非负整数$num$，对于所有的$i$，$0≤i≤num$，计算出$i$的二进制表示中1的个数。

进一步：

  • 计算量是$O(nlogn)$的算法很简单，你能否想出计算量是$O(n)$ 的算法?
  • 空间复杂度只能是$O(n)$；
  • 不可以使用C++中的__builtin_popcount等内建函数；

样例

1
2
输入：5
输出：[0,1,1,2,1,2]。

问题分析

(动态规划) $O(n)$

令f[i]表示 i的二进制表示中1的个数。

则f[i]可以由f[i/2]转移过来，i的二进制表示和⌊i/2⌋的二进制表示除了最后一位都一样，所以f[i] = f[i/2] + (i&1);

时间复杂度分析：总共有n个状态，每个状态进行转移的计算量是O(1)，所以总时间复杂度是O(n)。

C++代码

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> countBits(int num) {
    	int m=num.size();
    	vector<int> f(m);
    	for(int i=0;i<m;i++){
  			f[i]=f[i/2]+(i&1);   //如果i为奇数的话，那么i的二进制表示的数最后一位一定为0，右移后一定会少一个0
		}
		return f;
	}
};

问题五：Longest Increasing Path in a Matrix

问题描述

给定一个整数矩阵，请找到最长的上升路径。

对于矩阵中的每个格子，你每次可以走到上下左右四个方向，不能斜着走，也不能走出边界。

样例1

1
2
3
4
5
6
7
8
输入：nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
输出：4 
解释：最长的上升路径是：[1, 2, 6, 9].

样例2

1
2
3
4
5
6
7
8
输入：nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
] 
输出：4 
解释：最长的上升路径是：[3, 4, 5, 6]. 不能斜着走。

问题分析

(记忆化搜索，动态规划)$ O(n2)$

这是动态规划里非常经典的一道题目，几乎是所有学编程的同学都会遇到的一道题目。

假设我们从最低点开始走，每次只能往更高的格子走。
状态表示：f[i][j]表示走到(i,j)这个格子时的最大长度。
状态转移：枚举上下左右四个格子，如果某个格子(a,b)比当前格子低，则用该格子更新当前格子的最大长度：$f[i][j] = max(f[i][j], dp(a, b) + 1)$。

由于这道题目的状态依赖关系比较复杂，不容易用循环来求每个状态的值，所以可以用记忆化搜索来做：如果某个状态还没计算过，则递归计算该状态的值，如果某个状态计算过，那么直接返回该状态下的值。

时间复杂度分析：假设矩阵的边长是 $n$。则总共有$n^2$个状态，状态转移的计算量是常数，所以总时间复杂度是 $O(n2)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int n, m;
    vector<vector<int>> f, g;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    int dp(int x, int y)
    {
        if (f[x][y] != -1) return f[x][y];
        f[x][y] = 1;
        for (int i = 0; i < 4; i ++ )
        {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < n && b >= 0 && b < m && g[a][b] < g[x][y])
                f[x][y] = max(f[x][y], dp(a, b) + 1);
        }
        return f[x][y];
    }

    int longestIncreasingPath(vector<vector<int>>& matrix) {
        if (matrix.empty()) return 0;
        g = matrix;
        n = g.size(), m = g[0].size();
        f = vector<vector<int>>(n, vector<int>(m, -1));
        int res = 0;
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < m; j ++ )
                res = max(res, dp(i, j));
        return res;
    }
};

问题六：Coin Change

问题描述

给定 n 种不同硬币的面值，以及需要凑出的总面值 total。请写一个函数，求最少需要多少硬币，可以凑出 total的钱。
如果不存在任何一种拼凑方案，则返回-1。

注意：
你可以假定所有硬币都有无限多个。

样例1

1
2
3
输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

样例2

1
2
输入：coins = [2], amount = 3
输出：-1

问题分析

(动态规划) $O(nm)$

完全背包问题。

相当于有$n$种物品，每种物品的体积是硬币面值，价值是1。问装满背包最少需要多少价值的物品？

状态表示：$f[i]$ 表示凑出$ i$价值的钱，最少需要多少个硬币。

第一层循环枚举不同硬币，第二层循环从大到小枚举所有价值（由于每种硬币有无限多个，所以要从小到大枚举），然后用第$ i$种硬币更新 $f[i]：f[i] = min(f[i], f[i - coins[i]] + 1)$。

时间复杂度分析：令$n$表示硬币种数，$m$表示总价钱，则总共两层循环，所以时间复杂度是$O(nm)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
    	int n=coins.size();
    	vector<int> f(amount+1,amount+1);
    	f[0]=0;   //边界情况，当需要兑换的金额为0时
    	for(int i=1;i<=amount;i++)
    		for(int j=0;j<n;j++)
    			if(i>=coins[j]){
  					f[i]=min(f[i],f[i-coins[j]+1);
				}
		return (f[amount]>amount)? -1:f[amount];
	}
};

问题七：Maximal Square

问题描述

在一个只包含0和1的二维矩阵中，找到最大的正方形，使得正方形只包含1，返回正方形的面积。

样例

1
2
3
4
5
6
7
8
9
输入：二维01矩阵，如
[
    [1 0 1 0 0],
    [1 0 1 1 1],
    [1 1 1 1 1],
    [1 0 0 1 0]
]
输出：4
解释：可以看到最大的只包含1的正方形面积为4

问题分析

(动态规划) $O(n^2)$

其实这道题可以是一个动态规划问题，用dp[i][j]记录到达(i,j)位置所能组成的最大正方形的边长。

我们首先来考虑边界情况，也就是当i或j为0的情况，那么在首行或者首列中，必定有一个方向长度为1，那么就无法组成长度超过1的正方形，最多能组成长度为1的正方形，条件是当前位置为1。

而对于递推公式，对于任意一点dp[i][j]，由于该点是正方形的右下角，所以该点的右边，下边，右下边都不用考虑，关心的就是左边，上边，和左上边，只有当前(i, j)位置为1，dp[i][j]才有可能大于0，否则dp[i][j]一定为0。当(i, j)位置为1，此时要看dp[i-1][j-1], dp[i][j-1]，和dp[i-1][j]这三个位置，我们找其中最小的值，并加上1，就是dp[i][j]的当前值了，这个并不难想，毕竟不能有0存在，所以只能取交集，最后再用dp[i][j]的值来更新结果res的值即可。

时间复杂度分析：$O(n^2)$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
    	int m=matrix.size();
    	int n=matrix[0].size
    	if(matrix.empty()) return 0;
    	int res=0;
    	vector<vector<int>> f(m,vector<int>(n));
    	for(int i=0;i<m;i++)
    		for(int j=0;j<n;j++){
    			if(matrix[i][j]=='0')
    				f[i][j]=0;
    			else{
    				f[i][j]=1;
  					if(i&&j){
  						f[i][j]+=min(f[i-1][j],min(f[i-1][j-1],f[i][j-1]));		
					}
				res=max(res,f[i][j]);
				}
			}
		return res;
	}
};

问题八：Out of Boundary Paths

问题描述

在一个m x n的网格上有一个球，给定球的起点坐标(i, j)，你每次可以将这个球移动到四个方向（上下左右）相邻的格子上或者移出网格边界。然而，你最多可以移动N次。求出所有可以将球移出网格边界的路径数量。答案数可能很大，返回模$10^9+7$ 后的结果。

样例

1
2
输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6

解释:

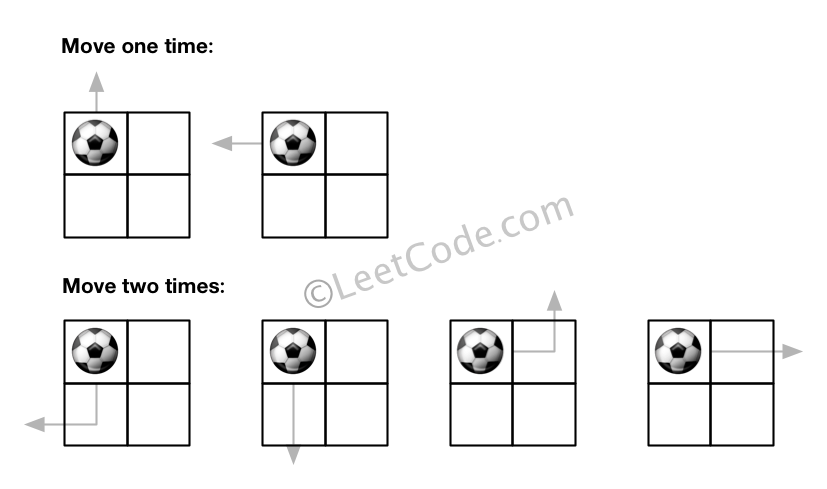
输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12

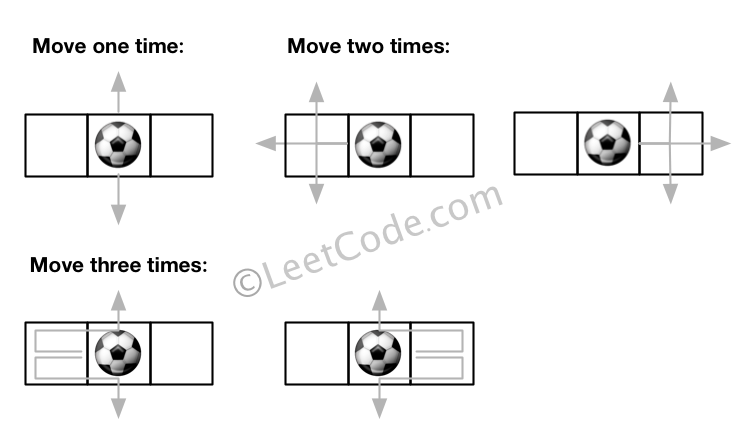
注意

  • 一旦将球移出网格边界，不可再移动回来。
  • 网格长和宽在 [1, 50] 的范围内。
  • N 在 [0, 50] 的范围内。

问题分析

(动态规划) $O(N⋅m⋅n)$

定义状态$f(k,x,y)$表示从网格边界格子经过$k$步，到达格子$(x, y)$的方案数。

初始时，每个位于边界的格子$(x, y)$，其$f(0,x,y)=1$；转移时，每个点可以从四个相邻的格子（如果存在）进行累加转移。

最终答案为，$f(0,i,j)+f(1,i,j)+…+f(N−1,i,j)$。由于规定边界的格子步数为 0，所以最多只能统计到 $N−1$步。

时间复杂度

状态数为$O(N⋅m⋅n)$，每个状态的转移数为$O(1)$，故总时间复杂度为$ O(N⋅m⋅n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
	vector<vector<vector<int>>> f;
	int mod=1000000007;
	int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};
	int findPaths(int m, int n, int N, int i, int j) {
		f=vector<vector<vector<int>>>(m,vector<vector<int>>(n,vector<int>(N,-1)));
		return dp(N,i,j);
	}
	int dp(int k,int x,int y){
  		int &v=f[x][y][k];
  		if(v!=-1) return v;
  		if(k==0) return 0;
  		v=0;
  		for(int i=0;i<4;i++){
  			int a=x+dx[i],b=y+dy[i];   //下一坐标
  			if(a<0||a>=m||b<0||b>=n)   //下一坐标能够出界
  				v++;
  			else
  				v+=dp(k-1,a,b);        //下一坐标不能够出界
		}
		return v;
	}
};

问题九：Decode Ways

问题描述

一个只包含 A-Z 的消息可以用如下方式编码成数字：

1
2
3
4
'A' -> 1
'B' -> 2
...
'Z' -> 26

给定一个只包含数字的非空字符串，返回共有多少种解码方案。

样例1

1
2
3
输入："12"
输出：2
解释：它可以被解码成 "AB" (1 2) 或者 "L" (12)。

样例2

输入："226"
输出：3
解释：它可以被解码成 "BZ" (2 26), "VF" (22 6),
    或者 "BBF" (2 2 6)。

问题分析

(动态规划)$ O(n)$

这道题目可以用动态规划来做。

状态表示：$f[i]$表示前$ i$个数字共有多少种解码方式。

初始化：0个数字解码的方案数1，即$f[0]=1$。

状态转移：$f[i]$可以表示成如下两部分的和：

  • 如果第 $i$个数字不是0，则 $i$个数字可以单独解码成一个字母，此时的方案数等于用前$i−1$个数字解码的方案数，即$ f[i−1]$；
  • 如果第$i−1$个数字和第$ i$个数字组成的两位数在$10$ 到$26$ 之间，则可以将这两位数字解码成一个字符，此时的方案数等于用前$ i−2$数字解码的方案数，即$ f[i−2]$；

时间复杂度分析：状态数是$ n$个，状态转移的时间复杂度是 $O(1)$所以总时间复杂度是 $O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int numDecodings(string s) {
      	if(s.empty()) return 0;
    	int m=s.size();
    	vector<int> f(m+1);
    	f[0]=1;
    	for(int i=1;i<=m;i++){
  			if(s[i]!='0')
  				f[i]+=f[i-1];
          	if(i>1){
  				int t=(s[i-2]-'0')*10+s[i-1]-'0';
              	if(t>=10&&t<=26)
                  	f[i]+=f[i-2];
			}
		}
      	return f[m];
	}
};

问题十：Ugly Number II

问题描述

找出第n大的“丑数”(ugly number)，其中，丑数是指质因数只有2、3、5的正整数。

样例

1
2
3
输入：10
输出：12
说明：从小到大列出丑数序列：1, 2, 3, 4, 5, 6, 8, 9, 10, 12...，其中12是第10个丑数，所以输出12

问题分析

（动态规划 指针）$O(n)$

由于丑数的因子也必定是丑数，它一定是某个丑数乘2、3、5得到的，因此我们可以采用动态规划的思想，利用前面已经得到的丑数序列来得到之后的丑数，而问题的关键在于如何确定状态转移方程。由于小的丑数乘5不一定比大的丑数乘2要小，我们没法直接使用目前最大的丑数来乘2、3、5顺序得到更大的丑数。不过，我们可以确定的是，小的丑陋数乘2，肯定小于大的丑陋数乘2。所以我们使用三个指针，分别记录乘2、3、5得出的目前最大丑陋数，而新的丑数就是这三个目前最大丑数中最小的那个，那么就需要更新被选中的丑数的指针，获得新的三个目前最大丑数，依次类推，从而得到最终结果。

时间复杂度分析：需要维护3个指针，从1到n遍历，复杂度为$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int nthUglyNumber(int n) {
    	vector<int> f(n);
    	f.push_back(1);
    	int i=0,j=0,k=0;
    	while(--n){
  			int t=min(f[i]*2,min(f[j]*3,f[k]*5));
  			f.push_back(t);
  			if(f[i]*2==t) i++;
  			if(f[j]*3==t) j++;
  			if(f[k]*5==t) k++;
		}
		return f.back();
	}
};

问题十一：Distinct Subsequences

问题描述

给定字符串 $S$ 和 $T$，统计$S$中有多少个不同的子序列和$T$相等。

字符串的子序列是指：将原字符串删掉若干字符后，其余字符相对顺序不改变，所得到的新串（例如：”ACE”是”ABCDE”的子序列，而”AEC”不是）

样例1

1
2
3
4
5
6
7
8
9
10
11
输入：S = "rabbbit", T = "rabbit"
输出：3
解释：如下所示，共有3种方案。
'^' 表示选择的字符

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

样例2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入：S = "babgbag", T = "bag"
输出：5
解释：如下所示，共有5种方案。
'^' 表示选择的字符

babgbag
^^ ^
babgbag
^^    ^
babgbag
^    ^^
babgbag
  ^  ^^
babgbag
    ^^^

问题分析

(动态规划) $O(nm)$

可以换一种考虑问题的方式：用中的字符，按顺序匹配$T$中的字符，问有多少种方式可以匹配完$T$中的所有字符。

可以用动态规划来做：
f[i][j]表示用$S$的前$i$个字符，能匹配完$T$的前$j$ 个字符的方案数。
初始化：因为$S$可以从任意一个字符开始匹配，所以f[i][0]=1,∀i∈[0,len(S)]。
状态转移：

  • 如果 S[i−1]≠T[j−1]，则 S[i−1] 不能匹配T[j−1]，所以f[i][j]=f[i−1][j]；
  • 如果S[i−1]=T[j−1]，则 S[i−1]既可以匹配 T[j−1]，也可以不匹配 T[j−1]，所以 f[i][j]=f[i−1][j]+f[i−1][j−1]；

边界情况：如果T为空串S不为空串，那么结果为1，如果T为空串S也为空串，那么结果也为1。

时间复杂度分析：假设 $S$的长度是 $n$ ，$T$的长度是 $m$，则共有$nm$个状态，状态转移的复杂度是 $O(1)$，所以总时间复杂度是$ O(nm)$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int numDistinct(string s, string t) {
    int m=s.size();
    int n=t.size();
    vector<vector<int>> f(m+1,vector<int>(n+1));
    
    for(int i=0;i<=m;i++) f[i][0]=1;
    
    for(int i=1;i<=m;i++)
    	for(int j=1;j<=n;j++){
  			f[i][j]=f[i-1][j];
  			if(s[i-1]==s[j-1])
  				f[i][j]+=f[i-1][j-1];
		}
	return f[m][n];
	}
};

问题十二：Palindrome Partitioning II

问题描述

给定一个字符串s，请将它划分成若干部分，使得每一部分都是回文串。
求最少需要切几刀。

样例

1
2
3
输入："aab"
输出：1
解释：可以划分成：["aa","b"]，所以只用切1刀。

问题分析

(动态规划) $O(n^2)$

一共进行两次动态规划。

第一次动规：计算出每个子串是否是回文串。

状态表示：st[i][j]表示 s[i…j]是否是回文串;
转移方程：s[i…j]是回文串当且仅当 s[i]等于s[j]并且 s[i+1…j−1]是回文串；
边界情况：如果s[i…j]的长度小于等于2，则st[i][j]=(s[i]==s[j]);

在第一次动规的基础上，我们进行第二次动规。

状态表示：$f[i]$ 表示把前 $i$个字符划分成回文串，最少划分成几部分；
状态转移：枚举最后一段回文串的起点$j$，然后利用$ st[j][i]$可知 $s[j…i]$是否是回文串，如果是回文串，则$f[i] $可以从$ f[j−1]+1$ 转移；

边界情况：0个字符可以划分成0部分，所以 $f[0]=0$。

题目让我们求最少切几刀，所以答案是 $f[n]−1$。

时间复杂度分析：两次动规都是两重循环，所以时间复杂度是 $O(n^2)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minCut(string s) {
    	int m=s.size();
    	vector<vector<bool>> st(m,vector<bool>(m));
    	for (int i = 0; i < n; i ++ )
            for (int j = i; j >= 0; j -- )
                if (i - j <= 1) st[j][i] = s[j] == s[i];
                else st[j][i] = s[j] == s[i] && st[j + 1][i - 1];
    	vector<int> f(m+1);
    	f[0]=0;
    	for(int i=1;i<=m;i++){
  			f[i]=INT_MAX;
  			for(int j=0;j<i;j++){
  				if(st[j][i-1])
  					f[i]=min(f[i],f[j]+1);
			}		
		}
      	return f[m]-1;
	}
};

问题十三： Predict the Winner

问题描述

给定一个非负整数的数组代表得分。有两个玩家A和B，玩家 A 先开始玩，可以从数组两端取出一个数作为自己的得分，然后玩家 B 接着从数组两端取出一个数作为自己的得分，再然后是玩家 A ，以此类推。每一次一个玩家取出一个数后，这个数就会消失。交替游戏知道所有的数字都被取走，得分高的玩家获胜。

给定一个数组，预测玩家 A 是否能获胜。假设两个玩家都采用最优策略。

样例

1
2
3
4
5
6
Input: [1, 5, 2]
Output: False
解释: 初始时，玩家 A 可以在 1 和 2 中选择。
如果他选择了 2 （或 1），则玩家B可以选择 1 （或 2）或者 5。如果玩家 B 选择了 5，则玩家A只剩下 1 （或 2）可以选。
所以，最终玩家 A 的得分是 1 + 2 = 3，玩家 B 是 5。
因此，玩家 A 永远都不可能获胜，应该返回 False。
1
2
3
4
Input: [1, 5, 233, 7]
Output: True
解释: 玩家 A 首先选择 1。接着玩家 B 只能在 5 和 7 之间选择。无论玩家B选择哪个数字，玩家 A 都可以选择 233。
最终，玩家 A (234) 比玩家 B (12) 有更多的分数，所以需要返回 True 代表玩家 A 可以获胜。

注意

  • 1 <= 数组长度 <= 20。
  • 数组中的非负整数不超过 10^7。
  • 如果最后两个玩家得分相同，则玩家 A 也是赢家。

问题分析

(动态规划) $O(n2)$

从最简单的问题开始考虑，假设只有一个数字，则只能玩家 A 选择这个数字。
接着，问题的规模开始扩大，扩大后，两个玩家会有两种决策，一种是选择数组头部，一种是选择数组尾部，而这两种情况下的子问题都可以提前计算出。至此，动态规划的思路已经很明显。
令 f(i,j)表示闭区间[i,j][i,j]下玩家 A 所能获得的最大分数。
每次 f(i,j) 转移有两种情况：

  • 当这一次是玩家 A 取数时，f(i,j)=max(f(i+1,j)+nums[i],f(i,j−1)+nums[j])表示从头部取或者从尾部取，二者最优；
  • 当这一次是玩家 B 取数时，玩家B肯定希望自己的得分最大，这必然会导致玩家 A 的得分变小，故此时f(i,j)=min(f(i+1,j),f(i,j−1))。

初始时，若最后一次是玩家 A 取数，则f(i,i)=nums[i]；否则f(i,i)=0。
最后玩家 A 能获得的最大得分就是f(0,n−1)。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> f(n, vector<int>(n, 0));

        int turn = n & 1;
        for (int i = 0; i < n; i++) {
            if (turn)
                f[i][i] = nums[i];
            else
                f[i][i] = 0;
        }

        for (int len = 2; len <= n; len++) {
            turn ^= 1;
            for (int i = 0; i < n - len + 1; i++) {
                int j = i + len - 1;
                if (turn)
                    f[i][j] = max(f[i + 1][j] + nums[i], f[i][j - 1] + nums[j]);
                else
                    f[i][j] = min(f[i + 1][j], f[i][j - 1]);
            }
        }

        return 2 * f[0][n - 1] >= accumulate(nums.begin(), nums.end(), 0);
    }
};
分享到： 收藏夹 复制网址 邮件 微信 QQ空间 腾讯微博 豆瓣 一键分享 更多