Leetcode贪心算法专题

问题一：Lemonade Change

题目描述

在柠檬水摊上，每一杯柠檬水的售价为5美元。

顾客排队购买你的产品，（按账单bills支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付5美元、10美元或20美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付5美元。

注意，一开始你手头没有任何零钱。

如果你能给每位顾客正确找零，返回true，否则返回false。

样例

输入：[5,5,5,10,20]

输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

输入：[5,5,10]

输出：true

输入：[10,10]

输出：false

输入：[5,5,10,10,20]

输出：false

解释：

前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。
注意
0 <= bills.length <= 10000
bills[i] 不是 5 就是 10 或是 20。

问题分析

(贪心) $O(n)$

• 开两个变量记录手中 5 元和 10 元的数量。

• 收到 5 元，直接增加一张 5 元；

• 收到 10 元，如果没有 5 元了，则返回 false；

• 收到 20 元，则如果有 10 元的，并且也有至少一张 5 元的，则优先将 10 元配 5 元纸币的找回（因为 5 元的可以更灵活）；如果没有 10 元的，但 5 元的有三张，则直接找回三张 5 元的。否则，无法找零，返回 false。

时间复杂度：只需遍历一次数组，故时间复杂度为$O(n)$。

空间复杂度：只需要常数个额外的变量，故空间复杂度为$O(1)$。

C++代码

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
    	int fives=0,tens=0;
    	for(auto m:bills){
  			if(m==5){
  				fives++;
			}
			else if(m==10){
  				if(fives)
  					fives--;
  					tens++;
  				else
  					return false;
			}
			else{
  				int t=15;   //需要找回15元
  				if(tens)
  					tens--;
  					t-=10;
  				while(t&&fives){
  					t-=5;
  					fives--;
				}
				if(t) return false;
			}
		}
		return true;
    }
};

问题二：Is Subsequence

问题描述

给定字符串s和t，判断s是否为t的子序列。

你可以认为s和t中仅包含英文小写字母。字符串t可能会很长（长度约为500,000），而s是个短字符串（长度 <=100）。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。例如，”ace”是”abcde”的一个子序列，而”aec”不是。

后续挑战 :

如果有大量输入的S，称作S1, S2, … , Sk 其中k >= 10亿，你需要依次检查它们是否为T的子序列。在这种情况下，你会怎样改变代码？

样例

Example 1:

输入: s = “abc”, t = “ahbgdc”
输出: true

Example 2:

输入: s = “axc”, t = “ahbgdc”
输出: false

问题分析

(贪心)$O(n)$

在一个for loop里访问一遍长字符串的每一位，逐个寻找s的每一位。

时间复杂度$O(n)$: 最多走一遍长字符串。

C++代码

class Solution {
public:
    bool isSubsequence(string s, string t) {
    	for(int i=0,j=0;i<s.size()&&j<t.size();j++){
  			if(s[i]==t[j])
  				i++;
		}
		return i==s.size();
    }
};

问题三：Assign Cookies

问题描述

假设你是一个英明的家长，想要给你的孩子们分配饼干。但是，你最多可以给每个孩子一块饼干。每个孩子$i$有一个贪心指数$g_i$ ，代表最少可以满足孩子的饼干大小。每块饼干$j$大小为$s_j$，如果$s_j≥g_i$，我们将饼干$j$给孩子 $i$，那么孩子$i$将会被满足。你的目标是最大化被满足孩子的数量。

样例

Input: [1,2,3], [1,1]

Output: 1

解释: 你有3个孩子和2块饼干。3个孩子的贪心指数分别为1, 2, 3。
而你只有2块饼干，每块大小为1，你只能满足贪心指数为1的孩子。
你需要输出1.

Input: [1,2], [1,2,3]

Output: 2

解释: 你有2个孩子和3块饼干。2个孩子的贪心指数分别为1, 2。
3块饼干的大小足够满足所有孩子。
你需要输出2。

问题分析

(贪心)$O(nlogn)$

• 分别将孩子的贪心指数和饼干尺寸都从小到大排序。

• 定义$i$和$j$从0开始，代表尝试将第$j$块饼干分配给第$i$个孩子。若$s_j>=g_i$，则答案加1，$i$和$j$都向后移动；否则 $j$向后移动（先满足期望值小的孩子）。

时间复杂度

排序的时间复杂度为$O(nlogn)$，遍历的过程为$O(n)$，故总时间复杂度为$O(nlogn)$。

C++代码

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
    	sort(g.begin(),s.end());
    	sort(s.begin(),s.end());    	
    	int res;
    	for(int i=0,j=0;i<s.size()&&j<g.size();i++){
  			if(s[i]>=g[j])
  				res++;
  				j++;
		}
		return res;
    }
};

问题四：Jump Game

问题描述

• 给定非负整型数组，初始时你在第一个元素的位置上。

• 每个元素代表每次可以跳跃的最大长度。

• 判断是否可以跳到数组末尾。

样例

Input: [2,3,1,1,4]
Output: true

Input: [3,2,1,0,4]
Output: false

问题分析

记录一个变量，记录你每次能够到达的最远距离

C++代码

class Solution {
public:
    bool canJump(vector<int>& nums) {
    	int dist=0;
    	for(int i=0;i<nums.size()&&i<=dist;i++){   //第二个条件表明之前有元素可以到达第i个位置
  			dist=max(dist,nums[i]+i);
		}
		return dist>=nums.size()-1;
	}
};

问题五：Jump Game II

问题描述

• 给定非负整型数组，初始时你在第一个元素的位置上。

• 每个元素代表每次可以跳跃的最大长度，求最少几步能跳到数组末尾。

• 数据保证能跳到数组末尾。

样例

Input: [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2.
    Jump 1 step from index 0 to 1, then 3 steps to the last index.

问题分析

(贪心递推)$ O(n)$

• 首先定义两个指针last和i，数组f[i]表示到达i所需要的最少步数。

• 定义last为第一次到达i时上一步的位置，last从0开始。

• 根据贪心得知，令f[i]=f[last]+1后，f[i]就会是最优值。

• 故可以根据i来让last向后移动，找到最早得可以一步到达i的位置，然后根据f[last]更新f[i]。

C++代码

class Solution {
public:
    int jump(vector<int>& nums) {
        int n=nums.size();
        vector<int> f;   
        f[0]=0;
        for(int i=1;i<n;i++){
            while(i>last+f[last])
                last++;
            f[i]=f[last]+1;
        }
        return f[n-1];
    }
};

问题六：Wiggle Subsequence

问题描述

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

进阶：
你能否用 O(n) 时间复杂度完成此题?

示例 1:

输入: [1,7,4,9,2,5]
输出: 6 
解释: 整个序列均为摆动序列。
示例 2:

输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。
示例 3:

输入: [1,2,3,4,5,6,7,8,9]
输出: 2

问题分析

• 首先对nums进行相邻去重，即用stl中的unique函数去除容器中相邻的重复元素（注意它是把重复元素放在容器末尾，返回值为去重之后的尾地址），再用erase函数进行删除

• 用一个for loop找极值点：如图，在一段连续上升（或下降）的线段中，只保留端点，可用反证法证明端点是最佳选择（如果选其他的，可能会使序列变短）。

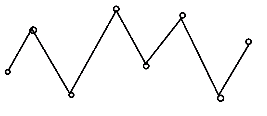
C++代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        nums.erase(unique(nums.begin(),nums.end()),nums.end());
        if(nums.size()<=2) return nums.size();
        int res=2;   //头尾两个元素肯定是包含的，只要计算第二个元素到倒数第二个元素
        for(int i=1;i+1<nums.size();i++){
            int a=nums[i-1],b=nums[i],c=nums[i+1];
            if(a>b&&c>b) res++;   //这两种情况下i对应的值为一个端点
            else if(a<b&&c<b) res++;
        }
        return res;
    }
};
//注意：unique只能去除相邻重复元素

问题七：Queue Reconstruction by Height

问题描述

假设你有一列随机的人在排队。每个人由一对整数(h, k)描述，其中h是这个人的高度，k是这个人前面的高度大于或等于h的人数。编写一个算法来重构队列。

样例

Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

问题分析

先将序列按照身高由高到低进行排序，身高相同的按照k值由低到高排序，先安排好身高比较高的人，每个人只能看到身高不低于自己的人，将每个人插到它相应的位置上

C++代码

bool cmp(pair<int,int>a,pair<int,int>b){
    return a.first>b.first||a.first==b.first&&a.second<b.second;
}   //按照身高从高到低进行排序，身高一样的按照k值进行排序，k越小越排在前面

class Solution {
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort(people.begin(),people.end(),cmp);   //先进行排序
        
        vector<pair<int,int>> res;
        for(auto p:people)
            res.insert(res.begin()+p.second,p);  //先安排那些身高比较高的，比他矮的人不管插在哪都不会影响
        return res;
    }
};

问题八：Minimum Number of Arrows to Burst Balloons

问题描述

有$n$个气球，每个气球用一个区间[x_start, x_end]表示，气球之间可能有重叠。一个飞镖可以发射到位置x，其可以戳破满足x_start <= x <= x_end的所有气球。气球最多有104104个。

返回最少的飞镖数，使得能戳破所有气球。

样例

Input:
[[10,16], [2,8], [1,6], [7,12]]

Output:
2

解释:
一种方式是发射 x = 6 和 x = 11 两个飞镖。

问题分析

(排序贪心) $O(nlogn)$
此题可以考虑将区间求交集，最后必定是一些不重叠的独立的区间，独立的区间个数就是答案数。具体做法如下：

• 首先将区间按照左端点从小到大排序，左端点相同的按照右端点从小到大排序。

• 设立两个值start和end代表当前飞镖可以放置的范围。

• 每当遇到一个新区间，若end小于新区间的起点，则需要一个新飞镖。否则原飞镖的区间start和新区间的起点取最大值，end和新区间的终点取最小值，即求交集。

时间复杂度

对所有区间排序一次，遍历一次，故总时间复杂度为$O(nlogn)$。

C++代码

class Solution {
public:
    int findMinArrowShots(vector<pair<int, int>>& points) {
    	if(points.size()==0) return 0;
    	sort(points.begin(),point.end());
    	int start=points[0].first,end=points[0].end();
    	int res=1;
    	for(int i=1;i<points.size();i++){
    		if(points[i].first<=end){
  				start=max(start,points[i].first);
  				end=min(end,points[i].second);
			}
			else{
  				start=points[i].first;
  				end=points[i].second;
  				res++;
			}
  			
		}
		return res;
    }
};

问题九：Remove K Digits

问题描述

给定一个用字符串表示的非负整数，从数字中删除k个数字，使新数字尽可能小。

num的长度小于10002，且≥k。

给定的num不包含任何前导零。

样本

Input: num = "1432219", k = 3
Output: "1219"
Explanation: Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.

Input: num = "10200", k = 1
Output: "200"
Explanation: Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.

Input: num = "10", k = 2
Output: "0"
Explanation: Remove all the digits from the number and it is left with nothing which is 0.

问题分析

由于最终的字符串的长度是一定的，理想情况下是数字按照从大到小的情况进行排序，那么只需要删除后面元素就可以了（最终需要处理字符串头部是否有0的情况）

利用栈的思想，依次扫描字符串中的每一个字符，如果扫描到的元素比栈顶元素大的话那么久直接压入栈，如果出现了逆序（也就是扫描到的元素比栈顶元素小），那么就直接将栈顶元素弹出，再进行比较，知道能够将扫描到的元素压入到栈

C++代码

class Solution {
public:
    string removeKdigits(string num, int k) {
        stack<char> stk;
        for (auto x : num)
        {
            while (stk.size() && stk.top() > x && k)
            {
                stk.pop();
                k--;
            }
            stk.push(x);
        }

        while (k -- ) stk.pop();

        string res;
        while (stk.size())
        {
            res += stk.top();
            stk.pop();
        }
        reverse(res.begin(), res.end());
        int i = 0;
        while (i < res.size() && res[i] == '0') i++;
        if (i == res.size()) return "0";
        return res.substr(i);
    }
};

问题十：Gas Station

问题描述

在一个环形公路上有N个加油站，第i个加油站有gas[i]单位的汽油。
你现在有一辆油箱大小不限的车，从第i个加油站到第(i+1)个加油站需要cost[i]升汽油。旅程开始时油箱为空，可以在任何的加油站作为起点。
如果你可以驾车顺时针完成一次环形旅行，则返回起始的加油站；否则返回-1。

注意

如果存在答案，题目保证存在唯一的答案。
两个数组都是非空的，且有相同的长度。
数组中每个元素都是非负整数。

样例

样例1

输入：
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出：
3

解释：
从第3个加油站开始，加4单位的汽油，目前邮箱有4单位汽油。
到第4个加油站，油箱为4 - 1 + 5 = 8
到第0个加油站，油箱为8 - 2 + 1 = 7
到第1个加油站，油箱为7 - 3 + 2 = 6
到第2个加油站，油箱为8 - 4 + 3 = 5
到第3个加油站，需要花费5个单位汽油，正好可以到达。
因此，输出为3。

样例2

输入：
gas  = [2,3,4]
cost = [3,4,3]

输出：
-1

问题分析

(贪心，双指针移动) $O(n)$
首先用gas-cost求出每一段的真正花费sum，然后将sum数组扩展为2*n，使得sum[i] == sum[i+n]。
定义两个指针start和end，分别表示当前假设的起点，和在这个起点下能走到的终点，tot为当前油量。
如果发现tot < 0，即不能走到end时，需要不断往后移动start，使得tot能满足要求。请读者在这里进行简要思考，向后移动start并不会使得[start,end]之间出现油量为负的情况。
如果end - start + 1 == n，即找到了一个环形路线。

时间复杂度

一共2 n个位置，每个位置最多遍历两次，故时间复杂度为*O(n)。

C++代码

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
    	int n=gas.size();
    	for(int i=0;i<n;i+=j+1)
    		int gas_left=0;
    		for(int j=0;j<n;j++){
    			int k=(i+j)%n;
  				gas_left+=gas[k]-cost[k];
  				if(gas_left<0)
  					break;
			}
			if(j>=n) return i;
		return -1;
	}
};