《剑指offer》 week2

发表于 | 分类于 ，

问题一：机器人的运动范围

题目描述

地上有一个$m$行和$n$列的方格，横纵坐标范围分别是 $0∼m−1$和$0∼n−1$。

一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格。

但是不能进入行坐标和列坐标的数位之和大于$k$的格子。

请问该机器人能够达到多少个格子？

样例1

1
2
3
输入：k=7, m=4, n=5

输出：20

样例2

1
2
3
4
5
6
输入：k=18, m=40, n=40

输出：1484

解释：当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。
      但是，它不能进入方格（35,38），因为3+5+3+8 = 19。

题目分析

(BFS) $O(nm)$
这是一个典型的宽度优先搜索问题，我们从 (0, 0) 点开始，每次朝上下左右四个方向扩展新的节点即可。

扩展时需要注意新的节点需要满足如下条件：

之前没有遍历过，这个可以用个$bool$数组来判断；

  • 没有走出边界；
  • 横纵坐标的各位数字之和小于$k$；
  • 最后答案就是所有遍历过的合法的节点个数。

时间复杂度

每个节点最多只会入队一次，所以时间复杂度不会超过方格中的节点个数。

最坏情况下会遍历方格中的所有点，所以时间复杂度就是$O(nm)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution{
public:
  	int get_Sum(pair<int,int> p){
  		int s=0;
      	while(p.first){
  			s+=p.first%10;
          	p.first/=10;
		}
      	while(p.second){
  			s+=p.second%10;
          	p.second/=10;
		}
      	return s;
	}
  	int getMoving(int rows,int cols,int threshold){
  		if(rows<0||cols<0||threshold<0) return 0;
      	queue<pair<rows,cols>> q;
      	vector<vector<bool>> st=vector<bool>(rows,vector<bool>(cols,false));
      	q.push({0,0});
      	int count=0;
      	int dx=[0,0,-1,1];
      	int dy=[1,-1,0,0];
      	while(q.size()){
  			auto cur=q.front();
          	q.pop();
          	if(st[cur.first][cur.second]||get_Sum(cur)>threshold) continue;
          	count++;
          	st[cur.first][cur.second]=True;
          	for(int i=0;i<4;i++){
  				int x=a+dx[i];
              	int y=b+dy[i];
              	if(x>=0&&x<=rows-1&&y>=0&&y<=cols) q.push({x,y});
			}
		}
      return count;
	}
}

总结

广度优先遍历思想：首先访问起始顶点v，然后由v出发，依次访问v的各个未访问的邻接顶点$w_1,w_2,…,w_i$，然后再依次访问$w_1,w_2,…,w_i$ 的所有的未被访问过的邻接顶点；再从这些访问过的顶点出发，再访问它们所有未被访问过的邻接顶点……依次类推，直到图中所有的顶点已经访问过。以这个题目为例，在每一步中，它的下一步访问节点是从这一步节点的上下左右四个方向选出一个位置来进行访问，然后基于这一步的下一步，再访问下一步的的下一步，因此是属于广度优先遍历的方法。

广度优先遍历是通过队列实现的，也就是先入先出，先来先服务

深度优先遍历思想：首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点$w_1$ ，再访问与$w_1$邻接且未被访问的任一顶点$w_2$，……重复上述过程。当不能再继续向下访问时1，依次退回到最近被访问过的顶点，若它还有未被访问过的顶点，则从该顶点开始重复上述的过程。week1里面的寻找数组中的路径就是利用的这种思想（主要就是在考虑当前步的时候要加上下一步的递归来进行判断）。

深度优先遍历是通过栈来实现的，也就是先进后出，先来后服务

问题二：剪绳子

题目描述

给你一根长度为$n$绳子，请把绳子剪成 $m$段（$m$、$n$都是整数，$2≤n≤58$ 并且 $m≥2$）。

每段的绳子的长度记为k[0]、k[1]、……、k[m]。k[0]k[1] … k[m] 可能的最大乘积是多少？

例如当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到最大的乘积18。

样例

1
2
3
输入：8

输出：18

题目分析

(数学) $O(n)$
这道题目是数学中一个很经典的问题。

下面我们给出证明：

首先把一个正整数$N$拆分成若干正整数只有有限种拆法，所以存在最大乘积。

假设 $N=n1+n2+…+nk$，并且$n1×n2×…×nk$是最大乘积。

显然1不会出现在其中；

如果对于某$i$有$n_i≥5$，那么把$n_i$拆分成 $3+(n_i−3)$，我们有 $3(n_i−3)=3n_i−9>ni$；

如果$n_i=4$，拆成 $2+2$乘积不变，所以不妨假设没有4；

如果有三个以上的2，那么$3×3>2×2×2$，所以替换成3乘积更大；

综上，选用尽量多的3，直到剩下2或者4时，用2。

时间复杂度分析

当$n$比较大时，$n$会被拆分成 $⌈n/3⌉$个数，我们需要计算这么多次减法和乘法，所以时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution{
public:
  	integerBreak(int n){
      	if(n<=3) return 1*(n-1);
      	int res=1;
      	if(n%3==1)   //若最后能够剩下4
          	res*=4;
      		n-=4;
      	else if(n%3==2){   //若最后能够剩下2
  			res*=2;
          	n-=2;
		}
      	while(n){
  			res*=res;
          	n-=3;
		}
      return res;
	}
}

总结

这个题目也可以用动态规划的思想解决

动态规划的问题具有以下几个特点：

  • 问题是求解一个最优解
  • 原始问题可以划分为许多的子问题，子问题中还具有相同的子问题
  • 原始问题的最优解可以有子问题的最优解得到

在这个问题中，可以划分为许多的子问题，比如$f(10)=f(4)*f(6)$ ，那么我们在分析问题的时候需要从上至下，在求解问题的时候需要从下至上。代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(){
 public:
 	integerBreak(int n){
  		int *len=new int[n+1];
  		len[0]=0;
  		len[1]=1;
  		len[2]=2;
  		len[3]=3;
  		int res;
  		for(int i=4;i<=n;i++){
  			int max=0;
  			for(int j=0;j<=i/2;j++){
  				if(len[j][j-i]>max)
  					max=len[j][i-j];
  			len[i]=max;
			}
		}
		res=len[n];
		return res;
	}
}

问题三：二进制中1的个数

题目描述

输入一个32位整数，输出该数二进制表示中1的个数。

注意：

  • 负数在计算机中用其绝对值的补码来表示。

样例1

1
2
3
输入：9
输出：2
解释：9的二进制表示是1001，一共有2个1。

样例2

1
2
3
4
输入：-2
输出：31
解释：-2在计算机里会被表示成11111111111111111111111111111110，
      一共有31个1。

题目分析

把一个整数 （无论正负或0）减去1，再和原整数做与运算，会把该整数最右边的一个1变为0，例如：110100减1后变为110011，二者进行与操作后，得到110000，最后边的1变为了0，而前面的位都不变。

这样，我们可以利用这这一结论来从左向右依次将整数的最右边的1变为0，当该整数的所有位为1的位均变为0之后，便统计到了该整数二进制中1的个数。

C++代码

1
2
3
4
5
6
7
8
9
10
class Solution{
public:
	int countOne(int n){
  		int count=0;
  		while(n){
  			count++;
  			n=n&(n-1);
		}
	}
}

总结

这个题目就是巧妙的利用了二进制中位运算进行分析。

变形的题目还有就是求两个整数m和n经过多少次二进制变换才能将m变换为n，这个就是先将m和n做异或操作，然后再将异或操作的结果作为二进制，计算出这个二进制中1的个数就可以。

问题四：数值的整数次方

题目描述

实现函数double Power(double base, int exponent)，求base的exponent次方。

不得使用库函数，同时不需要考虑大数问题。

注意：

  • 不会出现底数和指数同为0的情况

样例1

1
2
3
输入：10 ，2

输出：100

样例2

1
2
3
输入：10 ，-2  

输出：0.01

题目分析

这个题目的分析在week1中的斐波那契数中见过，就是使用快速幂的思想

时间复杂度分析

$O(log n)$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution{
public:
	double(double base,int exponent){
  		double ans=1;
  		while(exponent){
          	if(exponent&1!=0)
  				ans*=base;
  			base*=base;
  			exponent>>=1;
		}
		return ans;
	}
};

总结

这个题目重点在于对时间复杂度的考虑，常规的计算方法就是$O(n)$ 的时间复杂度。

常规的做法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    double Power(double a, int b) {
        double minus = 1;
        if (b < 0) minus = -1, b = -b;

        double res = 1;
        while (b -- ) res *= a;
        if (minus == -1) res = 1 / res;

        return res;
    }
};

问题五：在O(1)内的时间删除链表节点

题目分析

给定单向链表的一个节点指针，定义一个函数在O(1)时间删除该结点。

假设链表一定存在，并且该节点一定不是尾节点。

样例

1
2
3
4
输入：链表 1->4->6->8
      删掉节点：第2个节点即6（头节点为第0个节点）

输出：新链表 1->4->8

题目分析

这个题目就是在考虑时间复杂度下面下功夫，很显然常规的解法都是$O(n)$，废话不说，这个题目很简单

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void deleteNode(ListNode* node) {
        node->val=node->next->val;
        node->next=node->next->next;
    }
};

总结

其实吧，这个题目的条件很友善，说明删除的节点不是最后一节点，如果没有这个条件的话这个题目就会很复杂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void deleteNode(ListNode **pHead, ListNode* pDelNode) {
        if(pDelNode == NULL)
            return;
        if(pDelNode->next != NULL){
            ListNode *pNext = pDelNode->next;
            //下一个节点值赋给待删除节点
            pDelNode->val   =  pNext->val;
            //待删除节点指针指后面第二个节点
            pDelNode->next  = pNext->next;
            //删除待删除节点的下一个节点
            delete pNext;
            pNext = NULL;
        }else if(*pHead == pDelNode)//删除的节点是头节点
         {
            delete pDelNode;
            pDelNode= NULL;
            *pHead = NULL;
        } else//删除的是尾节点
        {
            ListNode *pNode = *pHead;
            while(pNode->next != pDelNode) {
                pNode = pNode->next;
            }
            pNode->next = NULL;
            delete pDelNode;
            pDelNode= NULL;
        }
    }

问题六：删除链表中数值重复的节点

题目描述

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留。

样例1

1
2
3
输入：1->2->3->3->4->4->5

输出：1->2->5

样例2

输入：1->1->1->2->3

输出：2->3

题目分析

(线性扫描) $O(n)$
为了方便处理边界情况，我们定义一个虚拟元素$dummy$指向链表头节点。
然后从前往后扫描整个链表，每次扫描元素相同的一段，如果这段中的元素个数多于1个，则将整段元素直接删除。

时间复杂度

整个链表只扫描一遍，所以时间复杂度是$O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        ListNode* p = dummy;
        while (p->next)
        {
            ListNode* q = p->next;   //这里的指针p记录的是上一段最后一个元素，q就是下一段的第一个元素
            while (q && q->val == p->next->val)
                q = q->next;
            if (p->next->next == q) p = p->next;   //这个时候就是q指针直接移动到了下下段的第一个元素
            else p->next = q;  //直接将中间的一段重复的元素给删除掉,因为p是上一段的元素，q是下下段的元素，中间有重复的元素
        }
        return dummy->next;
    }
};

问题七：正则表达式匹配

题目描述

请实现一个函数用来匹配包括'.'和'*'的正则表达式。

模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含0次）。

在本题中，匹配是指字符串的所有字符匹配整个模式。

例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但是与"aa.a"和"ab*a"均不匹配。

样例

输入：

s=”aa”
p=”a*”

输出:true

题目分析

这个题目是一个典型的动态规划问题。

转态转移：$f[i][j]$表示$s[i,…]$和$p[j,…]$相匹配

状态转移：

  • p[j]是正常字符，$f[i][j]$=s[i]==p[j]&&$f[i+1][j+1]$;
  • p[j]是”.”，$f[i][j]$=$f[i+1][j+1]$
  • p[j+1]是”*”，$f[i][j]=f[i+1][j]||f[i][j+2]$

C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>>f;
    int n, m;
    bool isMatch(string s, string p) {
        n = s.size();
        m = p.size();
        f = vector<vector<int>>(n + 1, vector<int>(m + 1, -1));   //初始化所有的二维数组为-1
        return dp(0, 0, s, p);
    }

    bool dp(int x, int y, string &s, string &p)
    {
        if (f[x][y] != -1) return f[x][y];    //由于是动态规划，所以有可能有的数组元素已经访问过了，用是否等于-1可以判断是否之前访问过
        if (y == m)    //走到了最后一格，递归的最后状态判断
            return f[x][y] = x == n;
        bool first_match = x < n && (s[x] == p[y] || p[y] == '.');   //先判断第一个元素是否匹配
        bool ans;
        if (y + 1 < m && p[y + 1] == '*')
        {
            ans = dp(x, y + 2, s, p) || first_match && dp(x + 1, y, s, p);
        }
        else
            ans = first_match && dp(x + 1, y + 1, s, p);
        return f[x][y] = ans;
    }
};

总结

这个题目在运用动态规划的时候要主要要使用一个数组记录已经访问过的元素，这里就是用到了数组f

问题八：表示数值的字符串

问题描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

例如，字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。

但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。

注意:

  1. 小数可以没有整数部分，例如.123等于0.123；
  2. 小数点后面可以没有数字，例如233.等于233.0；
  3. 小数点前面和后面可以有数字，例如233.666;
  4. 当e或E前面没有数字时，整个字符串不能表示数字，例如.e1、e1；
  5. 当e或E后面没有整数时，整个字符串不能表示数字，例如12e、12e+5.4;

样例：

1
2
3
输入: "0"

输出: true

题目分析

(模拟，字符串处理) $O(n)$
先去除行首和行尾空格；

行首如果有一个正负号，直接忽略；

如果字符串为空或只有一个’.’，则不是一个合法数；

循环整个字符串，去掉以下几种情况：

  • ‘.’或’e’多于1个;
  • ‘.’在’e’后面出现；
  • ‘e’后面或前面为空，或者’e’前面紧跟着’.’；
  • ‘e’后面紧跟着正负号，但正负号后面为空；

剩下的情况都合法；

时间复杂度分析

整个字符串只遍历一遍，所以时间复杂度是 $O(n)$。

C++ 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    bool isNumber(string s) {
        int i=0,j=s.size();
        while(i<=j&&s[i]==' ') i++;   //这里是将字符串中的所有的空格删去
        while(i<=j&&s[j]==' ') j--;
        if(i>j) return false;
        
        s=s.substr(i,j-i+1);  //从i位置开始，复制j-i+1个字符
        if(s[0]=='+'||s[0]=='-') s=s.substr(1);  //从1这个位置开始复制
        if(s.empty()||(s[0]=='.'&&s.size()==1)) return false;  //取出所有的  +,-,.这三种情况
        
        int dot=0;
        int e=0;
        for(int i=0;i<s.size();i++){
            if(s[i]>='0'&&s[i]<='9');
            else if(s[i]=='.'){
                dot++;
                if(dot>1||e) return false;  //12.12.12   12.12e12
            }
            else if(s[i]=='e'||s[i]=='E'){
                e++;
                if(!i||i+1==s.size()||e>1||(s[i-1]=='.'&&i==1)) return false;   //e123,123e,123e123e,.e123
                if(s[i+1]=='+'||s[i+1]=='-'){   //123e+,123e-
                    if(i+2==s.size()) return false;
                    i++;
                }
                
            }
            else return false;
        }
        return true;
    }
};

总结

就是考察自己细不细心，要学会进行调试代码

问题九：调整数组顺序使奇数位于偶数前面

题目描述

输入一个整数数组，实现一个函数来调整该数组中数字的顺序。

使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分。

样例

1
2
3
输入：[1,2,3,4,5]

输出: [1,3,5,2,4]

题目分析

(双指针扫描) $O(n)$

用两个指针分别从首尾开始，往中间扫描。扫描时保证第一个指针前面的数都是奇数，第二个指针后面的数都是偶数。

每次迭代时需要进行的操作：

  • 第一个指针一直往后走，直到遇到第一个偶数为止；
  • 第二个指针一直往前走，直到遇到第一个奇数为止；
  • 交换两个指针指向的位置上的数，再进入下一层迭代，直到两个指针相遇为止；

时间复杂度

当两个指针相遇时，走过的总路程长度是 $n$，所以时间复杂度是 $O(n)$。

C++代码

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    void reOrderArray(vector<int> &array) {
         int l = 0, r = array.size() - 1;
         while (l <= r) {
             while (array[l] % 2 == 1) l ++ ;
             while (array[r] % 2 == 0) r -- ;
             if (l < r) swap(array[l], array[r]);
         }
    }
};

总结

这个题目就是容易在l和r的取值上面犯错，不过可以在调试中解决，也算比较简单的一个题目。

问题十：找出链表中倒数第k各节点

问题描述

输入一个单链表，输出此链表中的倒数第 K 个节点。（去除头结点，节点计数从 1 开始）。

解法一：两次遍历法

解题思想

（1）遍历单链表，遍历同时得出链表长度 N 。

（2）再次从头遍历，访问至第 N - K 个节点为所求节点。

图解过程

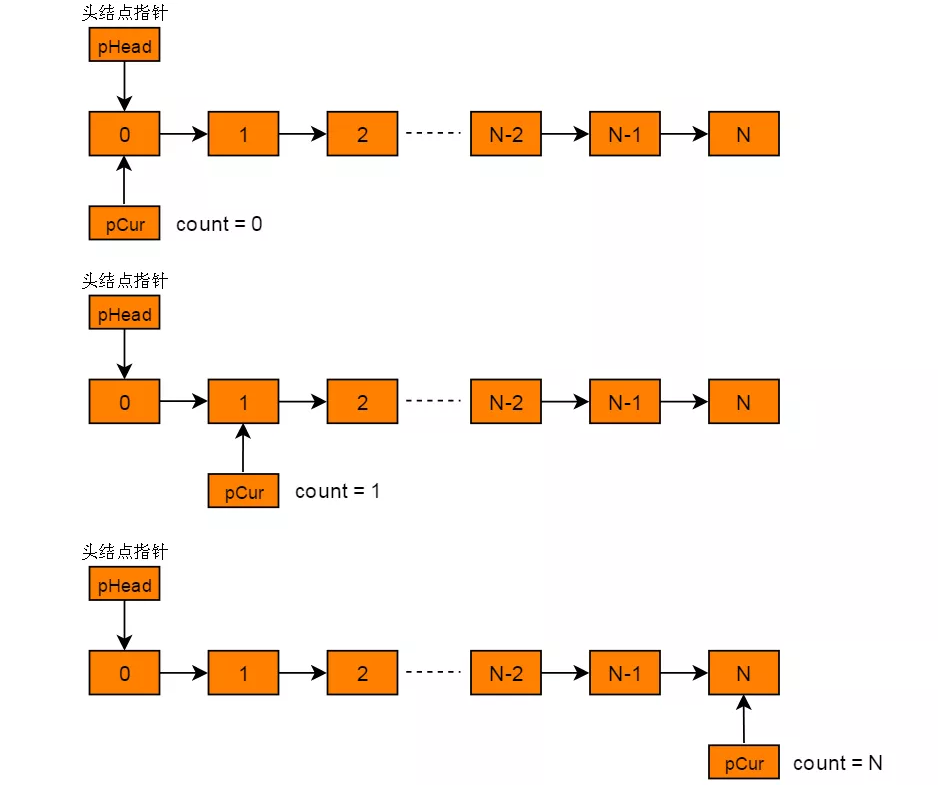
C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//计算链表长度
int ListLen(ListNode* pHead){
	ListNode* pcur=pHead;
	int count=0;
	while(pcur){
		pcur=pcur->next;
		count++;
	}
	return count;
}
ListNode* findK(ListNode* pHead,int k){
	int len=ListNode(pHead);
	int i=0;
	ListNode* pcur=pHead;
	//循环len-k+1次
	for(int i=0;i<len-k+1){
		pcur=pcur->next;
	}
	return pcur;
}

解法二：双指针法

解题思想

（1）定义两个指针 p1 和 p2 分别指向链表头节点。

（2）p1 前进K 个节点，则 p1 与 p2 相距 K 个节点。

（3）p1，p2 同时前进，每次前进 1 个节点。

（4）当 p1 指向到达链表末尾，由于 p1 与 p2 相距 K 个节点，则 p2 指向目标节点。

图解过程

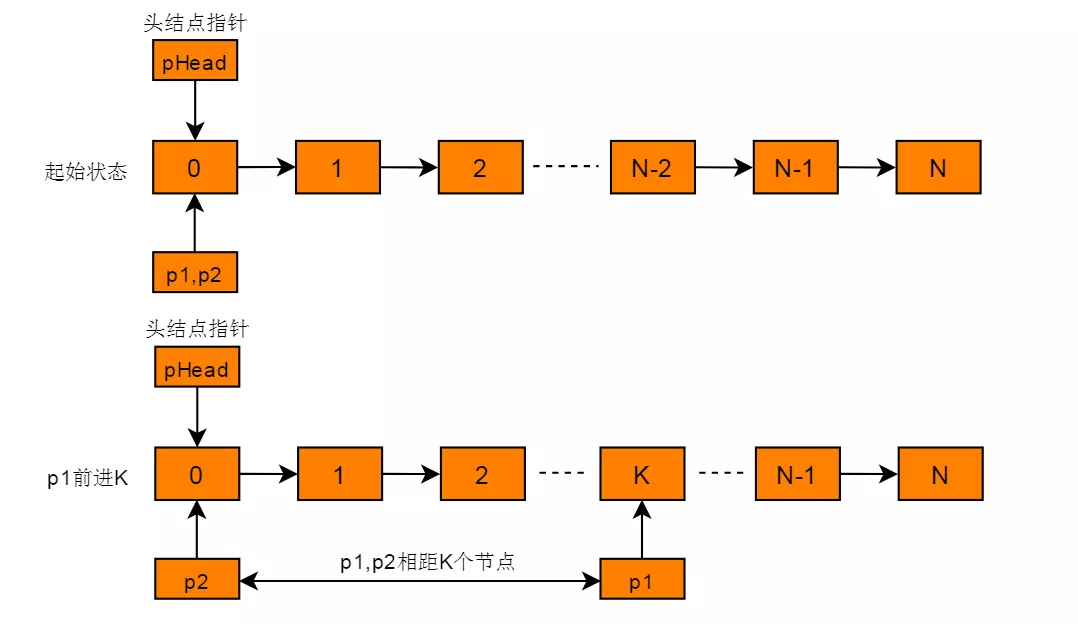
C++代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ListNode* findKthTail(ListNode *pHead, int K){
    if (NULL == pHead || K == 0)
        return NULL;
    //p1，p2均指向头节点
    ListNode *p1 = pHead;
    ListNode *p2 = pHead;
    //p1先出发，前进K个节点
    for (int i = 0; i < K; i++) {
        if (p1)//防止k大于链表节点的个数
            p1 = p1->_next;
        else
            return NULL;
    }
    while (p1)//如果p1没有到达链表结尾，则p1，p2继续遍历
    {
        p1 = p1->_next;
        p2 = p2->_next;
    }
    return p2;//当p1到达末尾时，p2正好指向倒数第K个节点
}

问题十一：链表中存在环的问题

快慢指针法（满指针走一步，快指针走两步）

总结

  • 如果不存在环的话，那么两个指针只能在链表末尾相遇；如果存在环的话，如果两个指针相遇且相遇的节点的狭义节点不是空节点的话，那么链表中肯定是有环的
  • 在定义环的入口的时候，只要分别定义两个指针，一个指针是从相遇的节点出发，一个是从头结点出发，这两个节点相遇的节点就是换的入口
  • 计算环的长度的时候，慢指针和快指针从相遇的节点出发，还是按照原来的规则进行遍历，当这两个指着再次相遇的时候慢指针走过的路径长度也就是换的长度

判断链表是否有环

解题思想

  • 定义两个指针分别为 slow，fast，并且将指针均指向链表头节点。
  • 规定，slow 指针每次前进 1 个节点，fast 指针每次前进两个节点。
  • 当 slow 与 fast 相等，且二者均不为空，则链表存在环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool isExistLoop(ListNode* pHead)  {  
    ListNode* fast;//慢指针，每次前进一个节点
    ListNode* slow;//快指针，每次前进2个节点 
    slow = fast = pHead ;  //两个指针均指向链表头节点
    //当没有到达链表结尾，则继续前进
    while (slow != NULL && fast -> next != NULL)  {  
        slow = slow -> next ; //慢指针前进一个节点
        fast = fast -> next -> next ; //快指针前进两个节点
        if (slow == fast)  //若两个指针相遇，且均不为NULL则存在环
            return true ;  
    }  
    //到达末尾仍然没有相遇，则不存在环
    return false ;  
}

定位环入口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//找到环中的相遇节点
ListNode* getMeetingNode(ListNode* pHead) // 假设为带头节点的单链表
{
    ListNode* fast;//慢指针，每次前进一个节点
    ListNode* slow;//快指针，每次前进2个节点 
    slow = fast = pHead ;  //两个指针均指向链表头节点
    //当没有到达链表结尾，则继续前进
    while (slow != NULL && fast -> next != NULL){  
        slow = slow -> next ; //慢指针前进一个节点
        fast = fast -> next -> next ; //快指针前进两个节点
        if (slow == fast)  //若两个指针相遇，且均不为NULL则存在环
            return slow;  
    }  

    //到达末尾仍然没有相遇，则不存在环
    return NULL ;
}
//找出环的入口节点
ListNode* getEntryNodeOfLoop(ListNode* pHead){
    ListNode* meetingNode = getMeetingNode(pHead); // 先找出环中的相遇节点
    if (meetingNode == NULL)
        return NULL;
    ListNode* p1 = meetingNode;
    ListNode* p2 = pHead;
    while (p1 != p2) // p1和p2以相同的速度向前移动，当p2指向环的入口节点时，p1已经围绕着环走了n圈又回到了入口节点。
    {
        p1 = p1->next;
        p2 = p2->next;
    }
    //返回入口节点
    return p1;
}

计算环的长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int getLoopLength(ListNode* head){
    ListNode* slow = head;
    ListNode* fast = head;
    while ( fast && fast->next ){
        slow = slow->next;
        fast = fast->next->next;
        if ( slow == fast )//第一次相遇
            break;
    }
    //slow与fast继续前进
    slow = slow->next;
    fast = fast->next->next;
    int length = 1;       //环长度
    while ( fast != slow )//再次相遇
    {
        slow = slow->next;
        fast = fast->next->next;
        length ++;        //累加
    }
    //当slow与fast再次相遇，得到环长度
    return length;
}

总结

休息了，近期不熬夜了。。。。。。

分享到： 收藏夹 复制网址 邮件 微信 QQ空间 腾讯微博 豆瓣 一键分享 更多