简介
神经网络近期的成功推动了模式识别和数据挖掘的研究,许多机器学习任务,例如目标检测,机器翻译,语音识别,曾经都严重依赖棘手的特征工程提取数据集的特征,现在已经被端到端的学习模式彻底改变,也就是卷积神经网络(CNN),长短时记忆网络(LSTM),和自编码(AE)。深度学习在许多领域的成功部分归功于快速发展的计算资源(如GPU)和大量训练数据,部分归功于深度学习从欧氏数据(如图像、文本和视频)中提取有效的数据表示。以图像分析为例,图像为欧式空间的规则表示,CNN能够利用图像数据的平移不变性,局部连结性和组合性,也就是CNN能够为各种图像分析任务提取整个数据集共享的局部特征。
深度学习在欧式数据上取得了巨大的成功,但是,越来越多的应用需要对非欧式数据进行分析。例如,在电子商务中,一个基于图的学习系统能够利用用户与商品之间的交互做出非常准确的推荐;在化学中,需要识别被建模为图结构的分子的生物活性以发现新的药物;在引文网络中,论文需要通过被引用的关系相互连接,然后通过挖掘关系被分成不同的组。图数据不规则,每个图的无序节点大小是可变的,且每个结点有不同数量的邻居结点,因此一些重要的操作如卷积能够在图像数据上轻易计算,但是不适用于图数据,可见图数据的复杂性给现有的机器学习算法带来了巨大的挑战 。此外,现有的机器学习算法假设数据之间是相互独立的,但是,图数据中每个结点都通过一些复杂的连接信息与其他邻居相关,这些连接信息用于捕获数据之间的相互依赖关系,包括,引用,关系,交互。
近年来,人们对扩展基于图数据的深度学习越来越感兴趣。在深度学习的驱动下,研究人员借鉴CNN,LSTM,深度AE的思想设计了图神经网路的架构。为了处理复杂的图数据,在过去几年中,对重要算子的泛化和定义发展越来越快。例如,图1说明了图卷积算子是如何受标准2-D卷积算子的启发的。

GNNS简史
图神经网络的表示法最早在Gori等(2005)[16]中提出,在Scarselli等(2009)[17]中进一步阐述。这些早期的研究通过迭代的方式,利用循环神经结构传播邻居信息,直到达到一个稳定的不动点,来学习目标节点的表示。这些过程计算代价大,因此很多研究在克服这些困难[18],[19].本文推广图神经网络术语表示所有的针对图数据的深度学习方法。
GNN的相关研究
相关的GNN综述很少,Bronstein et al.[8]使用几何深度学习的符号,概述了非欧式域的深度学习方法,包括图形和流形。因为是先驱性工作,所以漏掉了几个重要的基于空间的方法,包括[15]、[19]、[24]、[26]、[27]、[28]。此外,本研究未涵盖一些新开发的架构,而这些架构对于GCN同样重要。本文对图注意网络(GAN)、图的自动编码器(GAE)、图的生成网络(GGN)和图时空网络(GSTN)等学习范式进行了综合评述。 Battaglia等人[29]将位置图网络作为构建块学习关系数据,使用统一的框架对部分神经网络做了回顾。但是,这个泛化的网络高度抽象,对原始论文中的方法阐述不足。Lee等人[30]对GNN的分支GAT部分进行了总结。最近,张[31]等对GNN做了一个最近的研究,但是缺少对GGN和GSTN的研究。综上,现有GNN方面的综述都不完整。
GNN vs 网络嵌入
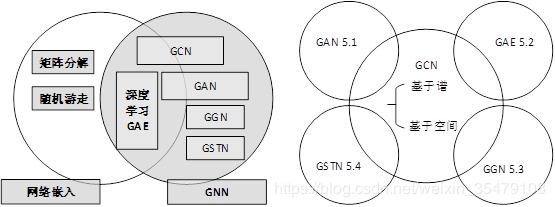
GNN的研究与图嵌入或网络嵌入密切相关,是数据挖掘和机器学习[32],[33],[34],[35],[36],[37]日益关注的另一个课题。网络嵌入致力于在一个低维向量空间进行网络节点表示,同时保护网络拓扑结构和节点的信息,便于后续的图像分析任务,包括分类,聚类,推荐等,能够使用简单现成的机器学习算法(例如,使用SVM分类)。许多网络嵌入算法都是典型的无监督算法,它们可以大致分为三种类型[32],即,矩阵分解[38]、[39]、随机游走[40]、深度学习。基于深度学习的网络嵌入属于GNN,包括图自编码算法,基于无监督训练的图卷积神经网络。图2描述了网络嵌入和GNN的区别。
GNN分类和框架
本节介绍文章对GNN分类的方法,将任何可微分模型(包含了神经结构)作为GNN。将GNN分为五种类型GCN,GAN,GAE,GGN,GSTN。其中GCN在捕获结构依赖性方面起到了重要作用,如图3所示,其他的方法都部分利用了GCN作为构建模型的块。表2总结了每一类方法的代表性方法。
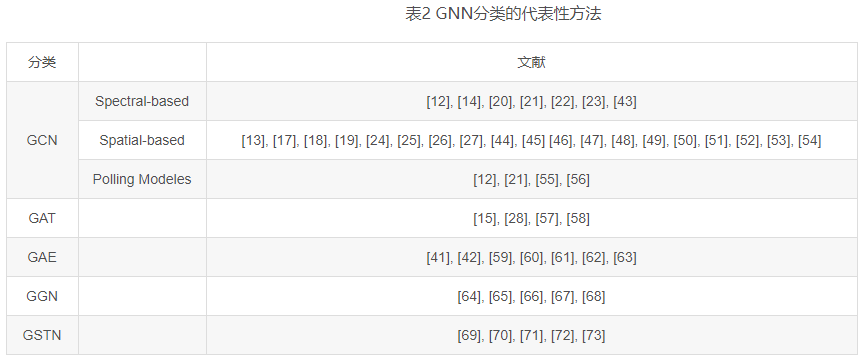
GNNs分类
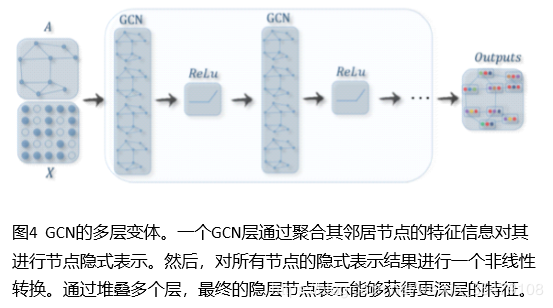
GCNs:GCNs将传统数据的卷积算子泛化到图数据,这个算法的关键是学习一个函数$f$,能够结合$v_i$邻居节点的特征$X_j$和其本身特征$X_i$生成$v_i$的新表示,$j∈N(v_i)$。图4展示了GCNs的节点表示学习。图5展示了一些基于GCN的图神经网络模型。
GAN:GAN与GCN类似,致力于寻找一个聚合函数,融合图中相邻的节点,随机游动和候选模型,学习一种新的表示。关键区别是:GAN使用注意力机制为更重要的节点,步或者模型分配更大的权重,权重个网络一起学习。图6展示了GCN和GAN在聚合邻居节点信息时候的不同。

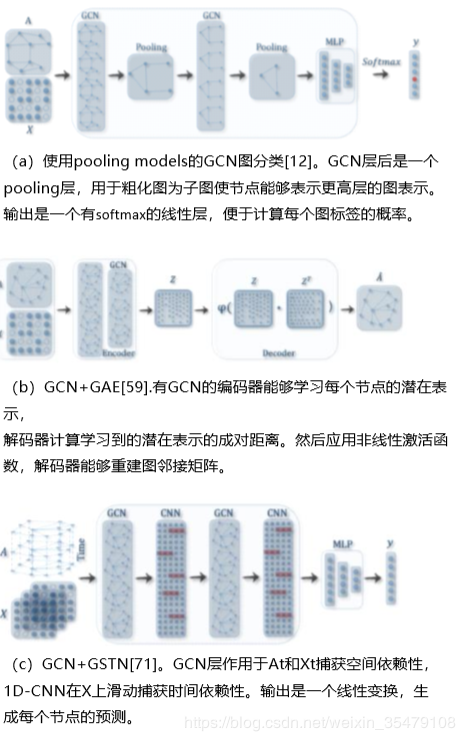
GAE:GAE是一种无监督学习框架,通过编码器学习一种低维点向量,然后通过解码器重构图数据。GAE是一种常用的学习图嵌入的方法,既适用于无属性信息[41]、[42]的普通图,还适用于是有属性图[61]、[62]。对于普通的图,大多数算法直接预先得到一个邻接矩阵,或者构建一个信息丰富的矩阵,也就是点对互信息矩阵,或者邻接矩阵填充自编码模型,并捕获一阶和二阶信息[42]。对于属性图,图自编码模型利用GCN[14]作为一个构建块用于编码,并且通过链路预测解码器[59],[61]重构结构信息。
GGN:GGN旨在从数据中生成可信的信息,生成给定图经验分布的图从根本上来说是具有挑战性的,主要因为图是复杂的数据结构。为了解决这个问题,研究员探索了将交替形成节点和边作为生成过程的因素,并借助[66],[67]作为训练过程。GGN一个很有前途的应用领域是化合物合成。在化学图中,视原子为节点,化学键为边,任务是发现具有一定化学和物理性质的可合成的新分子。
GSTN:GSTN从时空图中学习不可见的模式,在交通预测和人类活动预测等应用中越来越重要。例如,底层道路交通网络是一个自然图,其中每个关键位置是一个节点,它的交通数据是被连续监测的。通过建立有效的GSTN,能够准确预测整个交通的系统的交通状态[70],[71]。GSTN的核心观点是,同时考虑空间依赖性和时间依赖性。目前很多方法使用GCNs捕获依赖性,同时使用RNN[70],或者CNN[71]建模时间依赖关系。
框架
GNN,尤其是GCN,通过用谱图理论和空间局部性重新定义图卷积,试图在图数据上重复CNN的成功。使用图结构和节点信息作为输入,GCN的输出能够利用以下的一种机制用于不同的图分析任务:
- Node-level输出用于点回归和分类任务。图卷积模型直接给定节点的潜在表示,然后一个多层感知机或者softmax层用作GCN最后一层。
- Edge-level输出与边分类和链路预测任务相关。为了预测一条边的便签或者连接强度,附加函数从图卷积模型中提取两个节点的潜在表示作为输入。
- Graph-level输出和图分类任务相关,池化模块用于粗话一个图为子图或者对节点表示求和/求平均,以获得图级别上的紧凑表示。
端到端训练框架:GCN可以在端到端学习框架中进行(半)监督或无监督的训练,取决于学习任务和标签信息的可用性。
- node-level 半监督分类。给定一个部分节点被标记而其他节点未标记的网络,GCN可以学习一个鲁棒的模型,有效地识别未标记节点[14]的类标签。为此,可以构建一个端到端的多分类框架,通过叠加几个图形卷积层,紧跟着一个softmax层。
- graph-level 监督分类。给定一个图数据集,图级分类旨在预测整个图[55],[56],[74],[75]的类标签(s),端到端学习框架,通过结合GCN和池化过程[55,56]实现。具体的,通过GCN获得每个图里每个节点固定维数的特征表示,然后,通过池化求图中所有节点的表示向量的和,以得到整个图的表示。最后,加上多层感知机和softmax层,可以构造一个端到端的图分类。图5(a)展示了这样一个过程。
- 无监督图嵌入。图中没有标签数据的时候,可以在端到端的框架中以无监督的方式学习一种图嵌入。这些算法以两种方式利用边级信息。一种简单的:利用自编码框架,编码器利用GCN将图嵌入到潜在的表示中,解码器利用潜在的表示重构图结构[59,61]。另一种方式:利用负采样方法,抽取一部分节点对作为负对,图中剩余的节点对作为正对,之后利用逻辑回归层,形成一个端到端的学习框架[24]。
