正则化(Regularization)
机器学习中几乎都可以看到损失函数后面会添加一个额外项,常用的额外项一般有两种,一般英文称作$\ell_{1}$ -norm和$\ell_{2}-$ norm,中文称作L1正则化和L2正则化,或者L1范数和L2范数。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。下图是Python中Lasso回归的损失函数,式中加号后面一项$\alpha|w|_{1}$即为L1正则化项。
$\min _{w} \frac{1}{2 n_{\text {samples}}}|X w-y|_{2}^{2}+\alpha|w|_{1}$
下图是Python中Ridge回归的损失函数,式中加号后面一项$\alpha|w|_{2}^{2}$即为L2正则化项。
$\min _{w}|X w-y|_{2}^{2}+\alpha|w|_{2}^{2}$
一般回归分析中回归$w$表示特征的系数,从上式可以看到正则化项是对系数做了处理(限制)。L1正则化和L2正则化的说明如下:
- L1正则化是指权值向量$w$中各个元素的绝对值之和,通常表示为$|w|_{1}$
- L2正则化是指权值向量$w$中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为$|w|_{2}$
一般都会在正则化项之前添加一个系数,Python中用$\alpha$表示,一些文章也用$\lambda$表示。这个系数需要用户指定。
那添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择
- L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
稀疏模型与特征选择
上面提到L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。为什么要生成一个稀疏矩阵?
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
通过L1正则项来选择特征:L1正则方法具有稀疏解的特性,因此天然具备特征选择的特性,但是要注意,L1没有选到的特征不代表不重要,原因是两个具有高相关性的特征可能只保留了一个,如果要确定哪个特征重要应再通过L2正则方法交叉检验;应该是说,分别使用L1和L2拟合,如果两个特征在L2中系数相接近,在L1中一个系数为0一个不为0,那么其实这两个特征都应该保留,原因是L1对于强相关特征只会保留一个。
L1和L2正则化的直观理解
这部分内容将解释为什么L1正则化可以产生稀疏模型(L1是怎么让系数等于零的),以及为什么L2正则化可以防止过拟合。
L1正则化和特征选择
假设有如下带L1正则化的损失函数:
$J=J_{0}+\alpha \sum_{w}|w|$
其中$ J_0$是原始的损失函数,加号后面的一项是L1正则化项,$\alpha$是正则化系数。注意到L1正则化是权值的绝对值之和,$J$是带有绝对值符号的函数,因此$J$是不完全可微的。机器学习的任务就是要通过一些方法(比如梯度下降)求出损失函数的最小值。监督机器学习问题无非就是“minimizeyour error while regularizing your parameters”,也就是在规则化参数的同时最小化误差。当我们在原始损失函数$ J_0$后添加L1正则化项时,相当于对$J_0$做了一个约束。令$L=α∑w∣w∣ L = \alpha \sum_w{|w|}$,则$J=J_{0}+L$此时我们的任务变成在$L$约束下求出$J_0$取最小值的解.考虑二维的情况,即只有两个权值$w^1$和$w^2$ ,此时$L=\left|w^{1}\right|+\left|w^{2}\right|$,对于梯度下降法,求解$J_0$的过程可以画出等值线,同时L1正则化的函数$L$也可以在$w^1w^2$的二维平面上画出来。如下图:

图中等值线是$J_0$的等值线,黑色方形是$L$函数的图形。在图中,当$J_0$ 等值线与$L$图形首次相交的地方就是最优解。上图中$J_0$与$L$在$L$的一个顶点处相交,这个顶点就是最优解。注意到这个顶点的值是$(w^1,w^2)=(0,w) $。可以直观想象,因为L LL函数有很多『突出的角』(二维情况下四个,多维情况下更多),$J_0$与这些角接触的机率会远大于与$L$其它部位接触的机率,而在这些角上,会有很多权值等于0,这就是为什么L1正则化可以产生稀疏模型,进而可以用于特征选择。
而正则化前面的系数$\alpha$,可以控制$L$图形的大小。$\alpha$越小,$L$的图形越大(上图中的黑色方框);$\alpha$越大,$L$的图形就越小,可以小到黑色方框只超出原点范围一点点,这是最优点的值$(w^1,w^2)=(0,w)$ 中的$w$可以取到很小的值。类似,假设有如下带L2正则化的损失函数:
$J=J_{0}+\alpha \sum_{w} w^{2}$
同样可以画出他们在二维平面上的图形,如下:
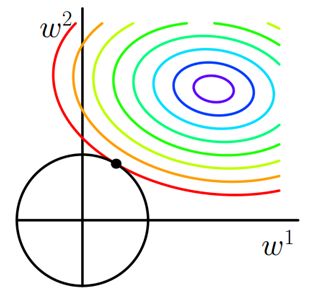
二维平面下L2正则化的函数图形是个圆,与方形相比,被磨去了棱角。因此$J_0$与$L$相交时使得$w^1$ 或$w^2$ 等于零的机率小了许多,这就是为什么L2正则化不具有稀疏性的原因。
L2正则化和过拟合
拟合过程中通常都倾向于让权值尽可能小,最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』。
那为什么L2正则化可以获得值很小的参数?
以线性回归中的梯度下降法为例。假设要求的参数为$\theta$,$h_{\theta}(x)$是我们的假设函数。线性回归一般使用平方差损失函数。单个样本的平方差是$\left(h_{\theta}(x)-y\right)^{2}$,如果考虑所有样本,损失函数是对每个样本的平方差求和,假设有$m $个样本,线性回归的代价函数如下,为了后续处理方便,乘以一个常数$\frac{1}{2 m}$:
$J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}$
在梯度下降算法中,需要先对参数求导,得到梯度。梯度本身是上升最快的方向,为了让损失尽可能小,沿梯度的负方向更新参数即可。
对于单个样本,先对某个参数$\theta_{j}$求导:
$\frac{\partial}{\partial \theta_{j}} J(\theta)=\frac{1}{m}\left(h_{\theta}(x)-y\right) \frac{\partial}{\partial \theta_{j}} h_{\theta}(x)$
注意到$h_{\theta}(x)$的表达式为$h_{\theta}(x)=\theta_{0} x_{0}+\theta_{1} x_{1}+\cdots+\theta_{n} x_{n}$。单个样本对某个参数$\theta_j$求导,$\frac{\partial}{\partial \theta_{j}} h_{\theta}(x)=x_{j}$,最终上式结果如下:
$\frac{\partial}{\partial \theta_{j}} J(\theta)=\frac{1}{m}\left(h_{\theta}(x)-y\right) x_{j}$
在考虑所有样本的情况,将每个样本对$\theta_j$的导数求和即可,得到下式:
$\frac{\partial}{\partial \theta_{j}} J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$
梯度下降算法中,为了尽快收敛,会沿梯度的负方向更新参数,因此在(3.3)式前添加一个负号,并乘以一个系数 $\alpha$(即学习率),得到最终用于迭代计算参数$\theta_j$的形式:
$\theta_{j} :=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$
其中$\alpha$是learning rate. 上式是没有添加L2正则化项的迭代公式,如果在原始代价函数之后添加L2正则化,则迭代公式会变成下面的样子:
$\theta_{j} :=\theta_{j}\left(1-\alpha \frac{\lambda}{m}\right)-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$
其中$\lambda$就是正则化参数。从上式可以看到,与未添加L2正则化的迭代公式相比,每一次迭代,$\theta_j$都要先乘以一个小于1的因子,从而使得$\theta_j$不断减小,因此总得来看,$\theta$是不断减小的。最开始也提到L1正则化一定程度上也可以防止过拟合。之前做了解释,当L1的正则化系数很小时,得到的最优解会很小,可以达到和L2正则化类似的效果。
正则化参数的选择
L1正则化参数
通常越大的$\lambda$可以让代价函数在参数为0时取到最小值。下面是一个简单的例子,这个例子来自Quora上的问答。为了方便叙述,一些符号跟这篇帖子的符号保持一致。假设有如下带L1正则化项的代价函数:
$F(x)=f(x)+\lambda|x|_{1}$
其中$x$是要估计的参数,相当于上文中提到的$w$以及$\theta$。 注意到L1正则化在某些位置是不可导的,当$\lambda$足够大时可以使得$F(x) $在$x=0$时取到最小值。如下图:
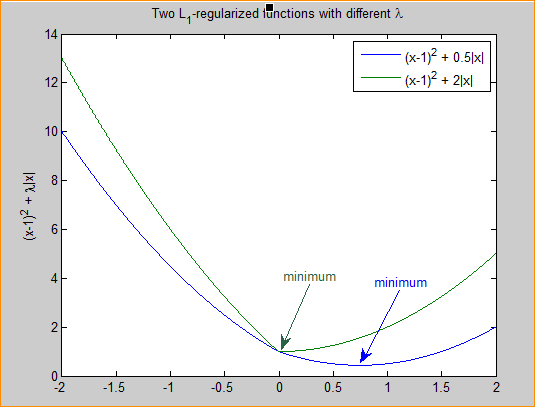
分别取$\lambda$ = 0.5和$\lambda$=2,可以看到越大的$\lambda$越容易使$F(x) $在$x=0$时取到最小值.
L2正则化参数
从公式5可以看到,$\lambda$越大,$\theta_j$衰减得越快。另一个理解可以参考图2,$\lambda$越大,L2圆的半径越小,最后求得代价函数最值时各参数也会变得很小。
