介绍

从交通优化、信息传播优化、用户网络分析，组合优化这一传统计算问题在日常应用中无处不在。然而，这类问题往往是NP难题（NP-hard），并需要大量的专业知识和试错来解决。在许多实际生活的应用中，相似的组合优化问题一次又一次的出现，而每次面对具有相同形式、但数据不同的问题，却需要大量人力一遍又一遍的设计新的算法方案。基于图的组合优化问题多年来受到理论和算法设计界的广泛关注。

传统的解决NP-hard图优化问题的方法主要有三种，下面介绍一下传统解决方案的不足：

精准算法：精准算法往往通过穷举或是基于整数规划的分支界限算法寻找问题的最优解，因此，这类算法无法被应用到数据规模较大的组合优化问题上。
近似算法：我们可以通过多项式时间的算法来近似最优解。现有的这类算法可被用来解决数据规模较大的组合优化问题，然而它们的最坏情况保证往往不尽如人意。另外，有部分问题是无法被近似解决的。
启发式搜索：启发式搜索指那些快速有效但缺乏理论支撑的算法。现有的这类算法的设计需要大量的专业知识和试错，因此无法被广泛使用。

这三种解决方案很少利用现实优化问题的一个共同特征：相似的组合优化问题一次又一次的出现，他们具有相同形式，而区别仅仅是数据的不同。换句话说，在许多应用中，每个问题的目标函数和限制都可以被当成是从某个概率分布中取出的样本。

比如，广告商如何在资源有限的情况下投放广告，使得广告信息在投放用户的相互传播后抵达尽可能多的人群？货运公司如何合理安排送货路线来提高送货效率？在社交网站的聚类分析中，我们如何根据每个用户的差异指数将用户分为两个用户组，从而最大化两个组之间的差异指数？

以上这些常见的问题都可以被归类为基于图论的组合优化问题（combinatorial optimization problems over graphs），这三个问题分别对应为最小顶点覆盖问题（minimum vertex cover, MVC）、最大割问题（maximum cut, MAXCUT）、巡回售货员问题（graph travelling salesman problem, GTSP）。

在这篇文章中，我们利用强化学习和图嵌入的独特结合来解决图问题的学习算法的挑战。学习到的策略的行为类似于一个元算法，它增量地构造一个解决方案，其行为由解决方案的当前状态上的图嵌入网络决定。更具体地说，这篇文章提出的解决方案框架与之前的工作在以下方面有所不同:

算法设计模式： 这篇文章将采用贪心元算法设计，根据图的结构，通过连续添加节点来构造可行解，并保持可行解，以满足问题的图约束。
算法的表示：我们将使用一个称为structure2vec的图嵌入网络来表示贪心算法中的策略。这种基于实例图的深度学习体系结构“特征化”了图中的节点，捕获了图邻居上下文中节点的属性。这允许策略根据节点的有用性在节点之间进行区分，并将其推广到不同大小的问题实例。
算法训练：我们将使用拟合Q-learning来学习由图嵌入网络参数化的贪心策略。该框架的建立使得策略能够直接优化原始问题实例的目标函数。

图上贪婪算法的常用公式

图的表示：$G(V;E;w)$ ，其中$V$ 表示的是图中的顶点结合，$E$ 表示的是图中边的集合，$w$ 表示的是每条边的权重。

下面介绍一下在这篇文章中提及到的三个经典图论问题：

最小顶点覆盖（MVC）： 给定一个N个点，M条边的无向图G（点的编号从1至N），问是否存在一个不超过K个点的集合S，使得G中的每条边都至少有一个点在集合S中。
最大分割问题（MAXCUT）: 给定一张图，求一种分割方法，将所有顶点（Vertex）分割成两群，同时使得被切断的边（Edge）数量最大。
货郎担问题（TSP）: 有一个售货员，从他所在城市出发去访问n-1个城市，要求经过每个城市恰好一次，然后返回原地，怎样规划才使得旅行路线最经济（即线路最短）。

贪心算法通过向部分解$S$中依次添加节点来构造一个解，它基于最大化某个评价函数$Q$来度量当前部分解节点的质量（也就是当前部分解是否是最优的）。

贪心法的好处：可以应对不同问题规模的图优化问题。

下面介绍一下本算法中的一些说明：

给定优化问题的问题实例$G$从分布$D$中采样，即实例图$G$的$V$、$E$和$w$是根据模型或真实数据生成的。
部分解用有序列表表示：$S = \left( v _ { 1 } , v _ { 2 } , \ldots , v _ { | S | } \right) , v _ { i } \in V$，$\overline { S } = V \backslash S$ 表示剩余可往部分解添加的候选节点，此外，我们使用二元决策变量$x$的向量，每个维度$x_v$ 对应于一个节点$v \in V , x _ { v } = 1$ 当且仅当$v \in S$，在其他情形下$x_v$=0。我们还可以将$x_v$视为$v$上的标记或额外特性。
函数$h(S)$将有序列表映射到满足问题特定约束的组合结构。
部分解$S$的性质由目标函数$c(h(S);G)$给出，该目标函数基于$S$的组合结构$h$。
一个通用的贪婪算法选择一个节点$v$来添加到部分解中，这个节点$v$可以最大化评价函数$Q ( h ( S ) , v )$ ，而评价函数是取决于基于当前部分解得到的组合结构$h(S)$ 。然后部分解就会扩展为$S : = \left( S , v ^ { \star } \right) ,$ where $v ^ { \star } : = \operatorname { argmax } _ { v \in \overline { S } } Q ( h ( S ) , v )$ ，$\left( S , v ^ { \star } \right)$ 表示将节点$v^{\star}$添加到部分解$S$中，这个步骤将会一直重复直到满足终止标准 $t ( h ( S ) )$ 。

具体算法如下：

这一算法的关键在于找到问题对应的评价函数Q。我们说一个评价函数Q*是最优的，当且仅当对任意一个问题具例，这个函数都能在此贪心算法下为我们找出最优解。通常情况下，寻找最优的评价函数这一任务本身就是NP难题，因此我们往往需要近似找出一个评价函数Q。解决这类问题的传统贪心算法需要算法设计人手动给出一个Q，（比如在最大割问题中，这个Q可以是节点的邻居数），而手动设计一个合理的评价函数在复杂问题中是不现实的。因此，这篇论文提出了用图嵌入寻找评价函数的方案。

将节点添加到部分解决方案$S$中所产生的解决方案质量的评估将由评估函数Q决定，该函数将使用问题实例的集合来学习。这与传统的贪心算法设计形成了鲜明的对比，在传统算法设计中，评价函数Q通常是手工制作的，需要对具体问题进行大量的研究和反复试验。接下来，我们将为评价函数设计一个强大的深度学习参数化$\widehat { Q } ( h ( S ) , v ; \Theta )$ ，参数为$\Theta$ 。

表示方法：图嵌入

$\widehat { Q }$应该总结这样一个“标记”的图G的状态，如果要在这样一个图的上下文中添加一个新节点，则应该计算出该节点的值。图的状态和节点v的上下文都非常复杂，很难用封闭的形式描述，可能依赖于复杂的统计信息，如全局/局部度分布、三角形计数、到标记节点的距离等。为了在组合结构上表示这种复杂的现象，我们将利用深度学习体系结构来表示图形，具体来说，此论文使用了structure2vec这一图嵌入网络。通过这一网络所寻找到的评价函数Q能够整合节点和它一步两步，甚至三步以外所有邻居的信息，并将这一信息压缩成一个有限维的非线性向量。具体算法如下，

Structure2Vec

structure2vec的计算图的灵感来自于图形模型推理算法，该算法根据$G$的图拓扑结构递归地聚合特定于节点的标记或特性$x_v$。在递归的几个步骤之后，网络将为每个节点生成新的嵌入，同时考虑图特征和这些节点特征之间的长期交互。structure2vec的一个变体将每个节点初始化嵌入$\mu _ { v } ^ { ( 0 ) }$ 为0，在每次迭代中同步更新嵌入$\mu _ { v } ^ { ( t + 1 ) } \leftarrow F \left( x _ { v } , \left\{ \mu _ { u } ^ { ( t ) } \right\} _ { u \in \mathcal { N } ( v ) } , \{ w ( v , u ) \} _ { u \in \mathcal { N } ( v ) } ; \Theta \right)$

其中$N(v)$为图$G$中节点$v$的邻域集合，F为神经网络或核函数等一般非线性映射。

根据更新公式可以看出，嵌入更新过程是基于图的拓扑结构进行的。只有在上一轮节点的所有节点的嵌入更新完成之后，才会开始一轮横扫节点的新一轮嵌入。很容易看到更新还定义了一个流程节点特征$x_v$传播到其他节点通过非线性传播函数$F$ .此外,更新迭代执行越多,节点信息传播得越广。在迭代$T$次后，我们可以得到每一个节点的嵌入$\mu _ { v } ^ { ( T ) }$。节点的嵌入是由图的拓扑、节点特征、传播函数$F$ 所决定的。下图展示了两个图的迭代嵌入。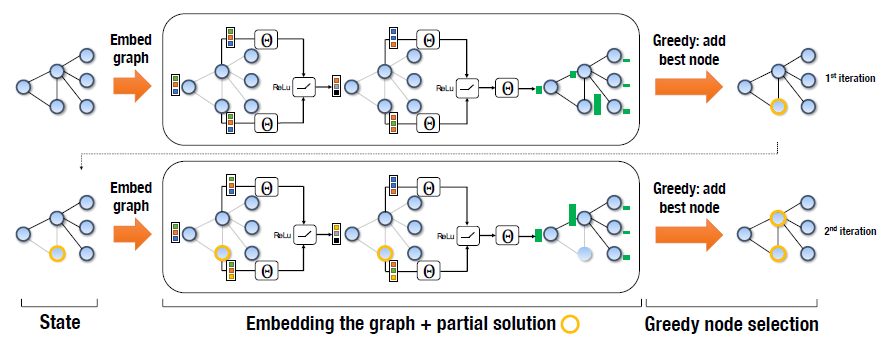

参数化Q函数

首先具体化了$F$函数:$\mu _ { v } ^ { ( t + 1 ) } \leftarrow \operatorname { relu } \left( \theta _ { 1 } x _ { v } + \theta _ { 2 } \sum _ { u \in \mathcal { N } ( v ) } \mu _ { u } ^ { ( t ) } + \theta _ { 3 } \sum _ { u \in \mathcal { N } ( v ) } \operatorname { relu } \left( \theta _ { 4 } w ( v , u ) \right) \right)$

对邻域求和是一种对邻域排列不变的邻域信息进行聚合的方法。为了便于说明，这里的$x_v$是前面描述的二进制标量;通过合并任何其他有用的节点信息，很容易将$x_v$扩展为向量表示形式。

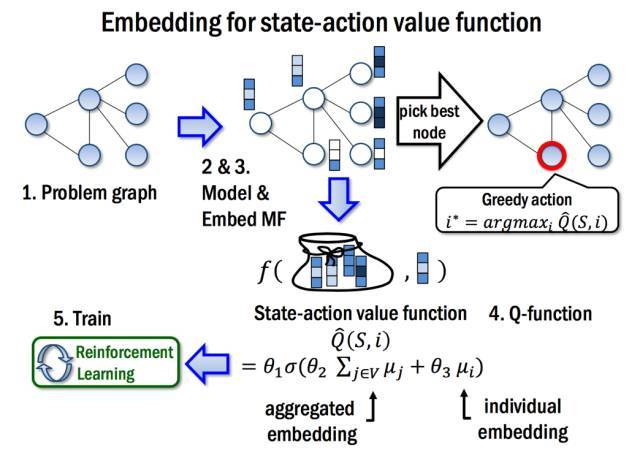
在T次迭代之后计算出每个节点的嵌入之后，我们将使用这些嵌入定义$\widehat { Q } ( h ( S ) , v ; \Theta )$ 函数。更具体地说，我们将使用节点$v$的嵌入$\mu _ { v } ^ { ( T ) }$以及整个图的集合嵌入，$\sum _ { u \in V } \mu _ { u } ^ { ( T ) }$ 作为$v$和$h(S)$ 的代替：$\widehat { Q } ( h ( S ) , v ; \Theta ) = \theta _ { 5 } ^ { \top } \operatorname { relu } \left( \left[ \theta _ { 6 } \sum _ { u \in V } \mu _ { u } ^ { ( T ) } , \theta _ { 7 } \mu _ { v } ^ { ( T ) } \right] \right)$

因为嵌入$\mu _ { u } ^ { ( T ) }$根据图嵌入网络的参数计算，$\widehat { Q } ( h ( S ) , v )$函数将由七个参数决定$\Theta = \left\{ \Theta _ { i } \right\} _ { i = 1 } ^ { 7 }$。图嵌入计算的迭代次数$T$通常较小，如$T$ = 4。算法的流程如下图所示

参数$\Theta$ 是需要学习到的，在这里，我们训练这些参数通过强化学习。

训练：Q-learning

由于$\widehat { Q }$ 很容易就可以和强化学习里面的状态价值函数联系在一起，所以我们很容器联想到强化学习。

强化学习介绍

状态：状态S是图G上节点的一个序列。状态是一个p维空间的向量。很容易看出，这种状态的嵌入表示可以跨不同的图使用。终端状态$\widehat { S }$取决于当前的问题;

转移：可以理解为当前状态下选取的节点$v$ 后到达下一个状态。

动作：动作$v$是不属于当前状态$s$的$G$节点，同样，我们将动作表示为其对应的嵌入$v$的$p$维节点，这种定义适用于各种尺寸的图形;

奖励：奖励函数$r(S;v)$状态S定义为采取行动v并转移到新状态后成本函数的变化$S ^ { \prime } : = ( S , v )$ ，定义为：$r ( S , v ) = c \left( h \left( S ^ { \prime } \right) , G \right) - c ( h ( S ) , G )$。因此，终端状态$\widehat { S }$的累积奖励R与$\widehat { S }$的目标函数值完全吻合，比如$R ( \widehat { S } ) = \sum _ { i = 1 } ^ { | \widehat { S } | } r \left( S _ { i } , v _ { i } \right)$=$c ( h ( \widehat { S } ) , G )$

策略：基于$\widehat { Q }$，采取的策略为$\pi ( v | S ) : = \operatorname { argmax } _ { v ^ { \prime } \in \overline { S } } \widehat { Q } \left( h ( S ) , v ^ { \prime } \right)$，选择动作$v$对应于在当前局部解中添加一个$G$节点，得到一个奖励$r(S;v)$。

学习算法

提出用强化学习中的n-step Q-learning这一方法来学习图嵌入网络的参数。n-step Q-learning的使用可实现强化学习中的延迟回报（这个部分没看懂）。

整体算法可被下图概括。

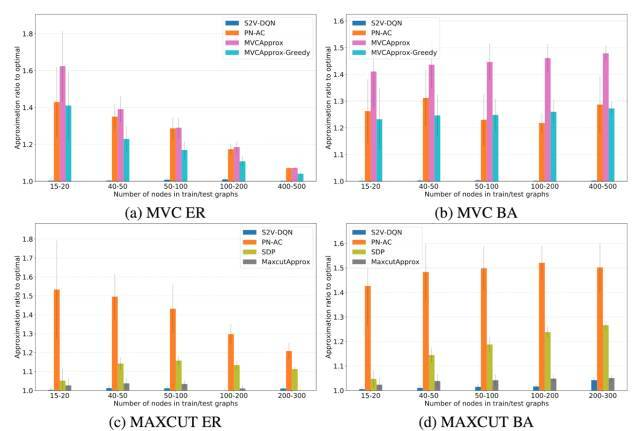
实证研究

此论文提出的新算法实现了基于图论的组合优化问题的“自动化”解决，那么这一算法的效率又如何呢？这篇论文将提出的新算法Structure2Vec Deep Q-learning和其他基于深度学习的算法（Pointer Networks With Actor-Critic）及近似/启发式算法作比较，发现这一算法所找出的解普遍更接近最优解（在下图中，approximation ratio越小表示解越优）。尤其是在MVC中，Structure2Vec Deep Q-learning得到解和最优解几乎没有差别（approximation ratio约等于1）。