线性可分支持向量机

给定一个特征空间上的训练数据集$\mathbb { D } = \left\{ \left( \vec { \mathbf { x } } _ { 1 } , \tilde { y } _ { 1 } \right) , \left( \vec { \mathbf { x } } _ { 2 } , \tilde { y } _ { 2 } \right) , \cdots , \left( \vec { \mathbf { x } } _ { N } , \tilde { y } _ { N } \right) \right\}$，其中

其中$\vec { \mathbf { x } } _ { i } \in \mathcal { X } = \mathbb { R } ^ { n } , \tilde { y } _ { i } \in \mathcal { Y } = \{ + 1 , - 1 \} , i = 1,2 , \cdots , N _ { 0 }$

$\vec { \mathbf { x } } _ { i }$为第$i$个特征向量，也称作实例；$\tilde { y } _ { i }$为$\vec { X } _ { i }$ 类的标记；$\left( \vec { \mathbf { x } } _ { i } , \tilde { y } _ { i } \right)$称作样本点。

当$\tilde { y } _ { i } = + 1$ 时，称$\vec { \mathbf { x } } _ { i }$为正例
当$\tilde { y } _ { i } = - 1$时，称$\vec { \mathbf { x } } _ { i }$ 为负例

假设训练数据集是线性可分的，则学习的目标是在特征空间中找到一个分离超平面，能将实例分到不同的类。

分离超平面对应于方程 $\vec { \mathbf { w } } \cdot \vec { \mathbf { x } } + b = 0$，它由法向量$\vec { \mathbf { w } }$和截距$b$ 决定，可以由$( \vec { \mathbf { w } } , b )$表示。

给定线性可分训练数据集，通过间隔最大化学习得到的分离超平面为：$\vec { w } ^ { \star } \cdot \vec { x } + b ^ { \star } = 0$，

相应的分类决策函数：$f ( \vec { \mathbf { x } } ) = \operatorname { sign } \left( \vec { \mathbf { w } } ^ { \star } \cdot \vec { \mathbf { x } } + b ^ { \star } \right)$，称之为线性可分支持向量机。

当训练数据集线性可分时，存在无穷个分离超平面可以将两类数据正确分开。

感知机利用误分类最小的策略，求出分离超平面。但是此时的解有无穷多个。
线性可分支持向量机利用间隔最大化求得最优分离超平面，这样的解只有唯一的一个。

支持向量

在训练数据集线性可分的情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量。

支持向量是使得约束条件等号成立的点，即$\tilde { y } _ { i } \left( \vec { \mathbf { w } } \cdot \vec { \mathbf { x } } _ { i } + b \right) - 1 = 0$：

对于正实例点，支持向量位于超平面 $H _ { 1 } : \vec { \mathbf { w } } \cdot \vec { \mathbf { x } } + b = 1$
对于负实例点，支持向量位于超平面$H _ { 2 } : \vec { \mathbf { w } } \cdot \vec { \mathbf { x } } + b = - 1$

超平面 $H _ { 1 } , H _ { 2 }$称为间隔边界，它们和分离超平面$\vec { \mathbf { w } } \cdot \vec { \mathbf { x } } + b = 0$平行，且没有任何实例点落在$H _ { 1 } , H _ { 2 }$之间。

在$H _ { 1 } , H _ { 2 }$之间形成一条长带，分离超平面位于长带的中央。长带的宽度称为$H _ { 1 } , H _ { 2 }$之间的距离，也即间隔（margin）

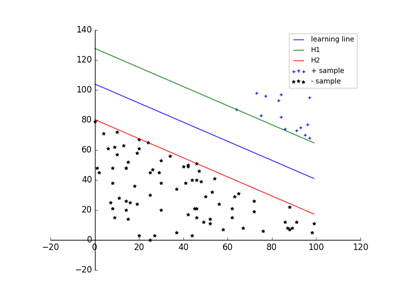
在决定分离超平面时，只有支持向量起作用，其他的实例点并不起作用。

如果移动支持向量，将改变所求的解。
如果在间隔边界以外移动其他实例点，甚至去掉这些点，则解是不变的。

由于支持向量在确定分离超平面中起着决定性作用，所以将这种分离模型称为支持向量机。

支持向量的个数一般很少，所以支持向量机由很少的、重要的训练样本确定。

点到直线的距离

假如有一个超平面，其数学表达式为 $\vec { \mathbf { w } } \cdot \vec { \mathbf { x } } + b = 0$ ，超平面上有两个点$x^{‘}$和$x^{‘’}$ 。

则$w^Tx^{‘}=-b$和$w^Tx^{‘’}=-b$ ，两式相减为$w^T(x^{‘}-x^{‘’})=0$ ，则$w$垂直于超平面。

在超平面外有一点$x$ ，求$x$到超平面的距离。

首先我们在超平面上任意选一个点$x^{‘}$，连接$x$和$x^{‘}$构成的向量投影于超平面，又由于$w$ 垂直于超平面，则点到超平面的距离为$\operatorname { distance } ( \mathbf { x } , b , \mathbf { w } ) = \left| \frac { \mathbf { w } ^ { T } } { | \mathbf { w } | } \left( \mathbf { x } - x ^ { \prime } \right) \right|$$\stackrel { ( 1 ) } { = } \frac { 1 } { | \mathbf { w } | } \left| \mathbf { w } ^ { T } \mathbf { x } + b \right|$

(1)是由于$w^Tx^{‘}=-b$

数学推导

由上面的论述得到支持向量机模型为：

目标函数： $\max _{ b , \mathbf { w } } \operatorname { margin } ( b , \mathbf { w } )$

约束条件：

$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) > 0$，$for\ all\ n$

$\operatorname { margin } ( b , w ) = \min _ { n = 1 , \ldots , N } \operatorname { distance } \left( \mathbf { x } _ { n } , b , w \right)=\min_{n=1,\ldots,N} \frac { 1 } { \| \mathbf { w } \| } \left| \mathbf { w } ^ { T } \mathbf { x } + b \right|$

接下来就是一步步的推导了，其实推导的过程就是将上述的目标条件和约束条件一步步简化。

将约束条件中的绝对值去掉

因为$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) > 0$，所以$\left| \mathbf { w } ^ { T } \mathbf { x } + b \right|=y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right)$

则目标条件： $\max _{ b , \mathbf { w } } \operatorname { margin } ( b , \mathbf { w } )$ ，

约束条件：

$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) > 0$，$for\ all\ n$

$\operatorname { margin } ( b , \mathbf { w } ) = \min _ { n = 1 , \ldots , N } \frac { 1 } { \| \mathbf { w } \| } y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right)$

将margin简化

我们知道$\mathbf { w } ^ { T } \mathbf { x } + b=0$ 和$\mathbf { 3w } ^ { T } \mathbf { x } + 3b=0$ 是相同的超平面，对于 $\min _ { n = 1 , \ldots , N }y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right)$ 我们肯定可以通过缩放使得 $\min _ { n = 1 , \ldots , N }y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right)=1$

这时$\operatorname { margin } ( b , \mathbf { w } )=\frac { 1 } { | \mathbf { w } | }$

因此目标函数： $\max _ { b , \mathbf { w } } \frac { 1 } { \| \mathbf { w } \| }$

约束条件：

$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) > 0 ,$ for all $n$
$\min _ { n = 1 , \ldots , N } y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) = 1$

去掉最小化min

假设新的约束条件为$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) \geq 1$ for all $n$

下面我们将采用反证法证明在新约束条件下得到的最优解$( b , \mathbf { w } ) $ 仍然满足旧约束条件 $\min _ { n = 1 , \ldots , N } y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) = 1$

假如我们新的约束条件为$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) > 1.126$ for all $n$ ，注意这里的1.126是任意一个比1大的数，也就是说这个约束条件肯定不包括$=1$ 的情况，则与我们的旧约束条件相违背，假设基于这个约束条件下得到一组最优解$( b , w )$ ，那么进而我们可以得到一个“更优”的解$\left( \frac { b } { 1.126 } , \frac { \mathrm { W } } { 1.126 } \right)$ ，这个时候我们发现这个解得到的目标函数“更优”，这里就推出来了矛盾（因为$( b , w )$ 解下的目标函数已经是最优的已经）！也就是说如果更换约束条件的话那么新的约束条件必然要包含1（小于1的情况可以不予以考虑）。

因此结合旧的约束条件我们可以将约束条件变换为$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) \geq 1$ for all $n$ ，这样的变换起到了放松约束条件但最优解不变的效果！

在这种条件下，目标函数： $\max _ { b , \mathbf { w } } \frac { 1 } { \| \mathbf { w } \| }$

约束条件：$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) \geq 1$ for all $n$

最大变最小

这一步很简单，也就是将目标函数中的最大变为最小，只需要将目标函数取一个倒数得到$| \mathbf { w } |$ ，这个式子的含义是向量$w$ 的模，最小化$| \mathbf { w } |$ 其实等价于$\frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w }$ （这里加一个0.5是方便计算）。

因此，目标函数： $\min _ { b , w } \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w }$

约束条件：$y _ { n } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } + b \right) \geq 1$ for all $n$

至此我们熟悉的支持向量机的求解模型就出来，当然，支持向量机还有其他形式的，待更…